Readings for Unit 7
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
Licensing Information

The readings for 6.s090 are licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. You are free to make and share verbatim copies (or modified versions) under the terms of that license.
Portions of these readings were modified or copied verbatim from the very nice book Think Python 2e by Allen Downey.
PDF of these readings also available to download: 6s090_reading7.pdf
Table of Contents
1) Introduction
Earlier in the course, we introduced the capability of function definition, which gave us the power to create functions that we could then abstract and treat as though they had been "built in" to Python. In the same way that we could use the built-in capabilities of, for example, addition or subtraction, we could create new variations on these operations and use them and treat them as though they had been defined as part of Python.
Turns out we can do the same thing, not with
procedures, but with data. Just like Python came with several
built-in operations and functions that we could then build on using
function definition, Python also comes with several built-in data
types (many of which you have experience with by now): int, float,
str, list, dict, and a few others. In this set of readings,
we'll explore a means for creating custom types of objects.
Then we'll take some time to explain a grab-bag of other Python features.
2) Classes and Instances
Way back in the first set of readings, we introduced objects as the main "things" that Python programs work with, and we noted that each object has both a type and a value: an object's value determines the exact thing it represents, and its type determines the kinds of things that programs can do to it (defines the set of valid operations on that type of object).
We will occasionally use different terminology: we can refer to an object's type as its class, and we can say that the object itself is an instance of that class.
For example, int is a class, and some examples of instances of that
class are: 478, 1, and 3. Similarly, str is a class, and some
examples of instances of that class are: "sandwich", "1234", and
"name".
By virtue of being members of the same class of objects, we can
operate on any string in exactly the same ways, regardless of the
particular value an instance represents; for example: we can
concatenate strings, we can use len to compute their length, we can
loop over them with for, we can index into them to find the
characters at particular locations within them, and we can convert
them to lowercase with x.lower(). Importantly, it is the object's
type that determines the operations that are possible when dealing
with that object.
By creating our own types (or classes) of objects, we will be able to treat
those custom data types as though they had been built in to Python. Throughout this reading, it will be important to draw a
distinction between creating a class of objects, and making an
instance of that class. When we talk about creating a class, we are
talking about defining a whole new type of objects (including both how
they are represented internally, and also the operations that are
possible for that class of objects); when we talk about making an
instance of a class, we are talking about making one particular
object. For example, list is a class, and when we type [1, 2, 3, 4]
into Python, we are making an instance of that class.
3) Custom Classes and Attributes
So far we've talked about this pretty abstractly; let's actually create our first class. Let's imagine that we are writing a program to perform some geometric calculations in 2-space.
In mathematical notation, points are often written in parentheses with a comma separating the coordinates. For example, (0,0) represents the origin, and (x,y) represents the point x units to the right and y units up from the origin.
There are several ways we might represent points in Python:
- We could store the coordinates separately in two variables,
xandy. - We could store the coordinates as elements in a list or tuple.
- We could create a new type to represent points as objects.
In some ways, creating a new type is more complicated than the other options, but it has advantages that we will see soon.
A programmer-defined type is also called a class, and is defined
using (perhaps unsurprisingly) the class keyword. Our first class
definition looks like this:
class Point:
pass
Class definitions always start with the class keyword, followed by a
name for the class (here, Point), followed by an indented body.
Class names are, by convention, capitalized.
For now, the body of this class definition is not particularly
interesting: it consists of a single instruction to Python: pass
(Python speak for do nothing). You can
define variables and functions inside a class definition, but we will
get back to that later.
Executing this definition causes Python to do two things: first, it
creates a class object to represent this class; and second, it
binds the name Point to this class object in the frame where the
class was defined.
As always, we'll need a way to represent these new things in our environment diagrams. We'll represent class objects similarly to how we represent frames or dictionaries, but with a note to indicate that they are indeed classes.
Evaluating the class definition above leaves us with the following
environment diagram (notice that this statement both created the class
object and associated the name Point with it):

When the class object is created, Python will execute the class body within that environment. It is possible to define variables within the class definition (typically, for things that are common to all instances of a class). For example, if we are only considering points in 2-space, we could have instead written:
class Point:
# using a short variable name to represent the number of
# coordinates so I can fit it in the environment diagram
n = 2
which would result in the following environment diagram:

We can look up and/or modify attributes within a class using the same dot notation we used for modules. For example, we could use the following:
print(Point.n)
To evaluate this expression, Python first looks up the name Point
(finding the class object), and then it looks up the name n inside
that object, finding the integer 2. We could also perform assignment
using similar notation:
Point.n = 3 # replaces the variable n inside the class
3.1) Creating Instances of User-Defined Classes
The class object is like a factory for creating objects. To create a
Point, you call Point as if it were a function.
blank = Point()
The return value is a reference to a Point object, which we assign to
blank. Creating a new object is called instantiation, and the
object is an instance of the class.
We'll represent instances of user-defined classes in a similar fashion, except that we will label them as instances, and their parent pointers point back to their associated class. So evaluating the line above would result in the following environment diagram:

3.2) Attributes
You can assign values to an instance of a user-defined class using dot notation, the same way you would assign them within a class:
blank.x = 3.0
blank.y = 4.0
This syntax is similar to the syntax for selecting a variable from a
module, such as math.pi or string.whitespace. In this case,
though, we are assigning values to named elements of an object.
These elements are called attributes1 or instance variables.
The following diagram shows the result of executing these statements:
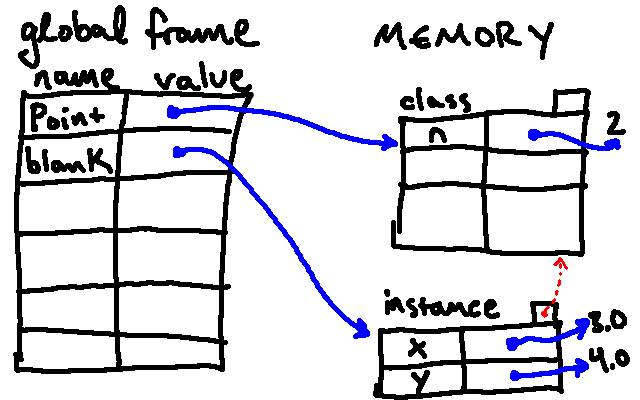
The variable blank refers to a Point object, which
contains two attributes. Each attribute refers to a
floating-point number.
You can read the value of an attribute using the same syntax:
print(blank.y) # prints 4.0
x = blank.x
print(x) # prints 3.0
Like we saw above with classes, the expression blank.x means "look up
the name blank in the current frame, and look up the name x inside
that object." In the example, we assign that value to a variable named
x. There is no conflict between the variable x and the attribute
x (because one is defined in the global frame, but the other is
defined inside the instance).
You can use dot notation as part of any expression. For example:
print('(', blank.x, ',', blank.y, ')') # prints ( 3.0 , 4.0 )
import math
distance = math.sqrt(blank.x**2 + blank.y**2)
print(distance) # prints 5.0
Notice that when we made our instance, we gave it a parent pointer to
the class in which it was defined. With the syntax blank.x, we looked
up the value of the name x inside the instance we had created. But
what happens if we try to look up a name that does not exist?
What happens when you look up blank.a? What about blank.n?
blank.a gives a new type of error: an AttributeError,
saying that this object has no attribute a. Looking up blank.n,
on the other hand, gives us 2.If Python is looking inside an object for an attribute and can't find
it, it will look next in that object's class for that name. If it
doesn't find it there, it will give an AttributeError (note that it
will not continue looking beyond the class; i.e., it will not look in
the global frame).
3.3) Example: Rectangles
Sometimes it is obvious what the attributes of an object should be, but other times you have to make decisions. For example, imagine you are designing a class to represent rectangles. What attributes would you use to specify the location and size of a rectangle? You can ignore angle; to keep things simple, assume that the rectangle is either vertical or horizontal.
There are at least two possibilities:
- You could specify one corner of the rectangle (or the center), the width, and the height.
- You could specify two opposing corners.
At this point it is hard to say whether either is better than the other, so we'll implement the first one, just as an example.
Here is the class definition:
class Rectangle:
pass
It doesn't look like much for now (because the body doesn't do anything).
Draw the environment diagram that results from executing this statement, assuming that all of the below code has also been executed.
class Point:
n = 2
blank = Point()
blank.x = 3.0
blank.y = 4.0
class Rectangle:
pass

To represent a particular rectangle, you have to instantiate a Rectangle object and assign values to the attributes:
box = Rectangle()
box.width = 100.0
box.height = 200.0
box.corner = Point()
box.corner.x = 0.0
box.corner.y = 0.0
The expression box.corner.x means: "Go to the object box refers to
and look up the attribute named corner; then go to that object and
look up the attribute named x."
Draw the environment diagram that results from executing the statements above.
First, we create an instance of Rectangle and associated it
with the name box in the global frame. Then we associate attributes
width and height inside this instance with values 100.0 and
200.0, respectively. Finally, we make a new instance of Point,
associate it with the name corner inside the Rectangle instance,
and associate attributes x and y in that (Point) instance with the
values 0.0 and 0.0, respectively.
It's starting to look a little like a bowl of spaghetti, but in the end, this results in the following diagram:
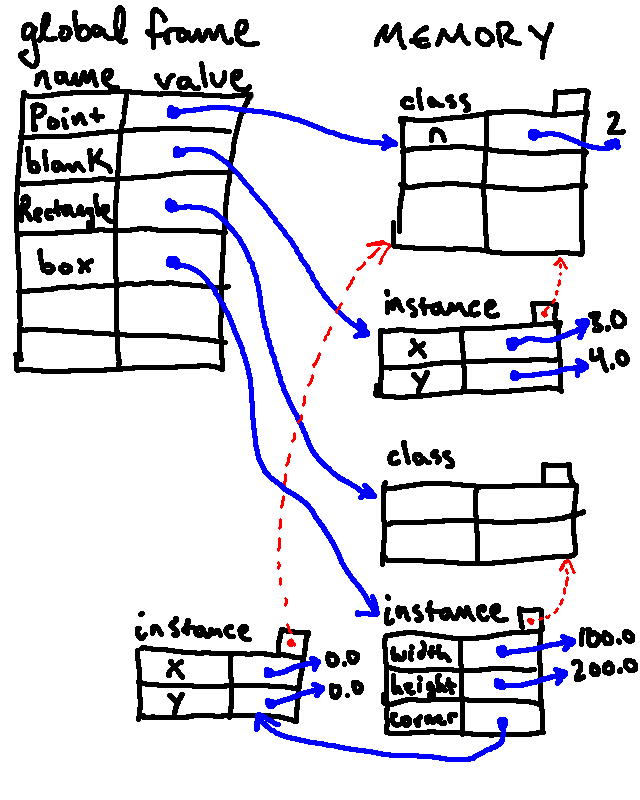
Using the environment diagram above, predict what will print to the screen if we run each of the following:
print(box.width)
print(box.corner.x)
print(box.corner.n)
print(box.corner.box)
print(box.x)
- The first will look up the name
boxin the global environment and then look up the namewidthinside that object, finding100.0. - The second will look up the name
boxin the global environment, look up the namecornerinside that object, and look up the namexinside that object, finding0.0. - The third will look up the name
boxin the global environment, look up the namecornerinside that object, and look up the nameninside that object. It does not findninside of that object, so it looks inside its class (Point) and finds the value2. - The fourth will not print anything, but will result in an error. Looking up
box.cornerfinds thePointinstance we created. We try to look up the nameboxinside that object and find nothing, so we look inside the class. In the class, we again don't find anything calledbox, so we give up and return an error. Importantly, we don't look for the nameboxin the global environment. - The last will also result in an error, because the name
xdoes not exist in the instance referred to bybox, nor in its class (Rectangle).
4) Classes and Functions
We saw in the previous section that instances of user-defined classes can be treated like primitive objects. This means that we can also make functions that operate on instances, or that return new instances.
Functions can return instances of user-defined classes. For example,
find_center defined below takes a Rectangle as an argument and
returns a Point that contains the coordinates of the center of the
Rectangle:
def find_center(rect):
p = Point()
p.x = rect.corner.x + rect.width/2
p.y = rect.corner.y + rect.height/2
return p
Here is an example that passes box as an argument and assigns
the resulting Point to center:
center = find_center(box)
def print_point(p):
print('(', p.x, ',', p.y, ')')
print_point(center) # prints ( 50 , 100 )
4.1) Functions that Modify Objects
We saw in the previous sections that objects are mutable. You can
change the state of an object by making an assignment to one of its
attributes. For example, to change the size of a rectangle without
changing its position, you can modify the values of width and
height:
box.width = box.width + 50
box.height = box.height + 100
You can also write functions that modify objects. For example,
grow_rectangle takes a Rectangle object and two numbers, dwidth
and dheight, and adds the numbers to the width and height of the
rectangle:
def grow_rectangle(rect, dwidth, dheight):
rect.width = rect.width + dwidth
rect.height = rect.height + dheight
Here is an example that demonstrates the effect:
print(box.width, box.height) # prints 150.0 300.0
grow_rectangle(box, 50, 100)
print(box.width, box.height) # prints 200.0 400.0
So how did this come to be? It's going to be a bit messy, but let's take a look at the environment diagram:
Write a function named move_rectangle that takes an instance of
Rectangle and two numbers named dx and dy. It should change the
location of the rectangle by adding dx to the x coordinate of
corner and adding dy to the y coordinate of corner.
Here is one solution:
def move_rectangle(rect, dx, dy):
rect.corner.x = rect.corner.x + dx
rect.corner.y = rect.corner.y + dy
4.2) Pure Functions
It is also possible to define pure functions involving instances (that is, functions that do not modify their arguments, but return a new result).
For example, we could write a function like move_rectangle, but
which creates a new instance representing the moved rectangle, rather
than mutating its input:
def shifted_rectangle(rect, dx, dy):
new_rect = Rectangle() # make a new instance
# height and width should be the same
new_rect.width = rect.width
new_rect.height = rect.height
# the corner of the rectangle is different, however
new_rect.corner = Point() # importantly, make a new instance of Point for the corner
new_rect.corner.x = rect.corner.x + dx
new_rect.corner.y = rect.corner.y + dy
return new_rect
5) Classes and Methods
In the previous section, we saw examples of functions that operate on
instances we've created. Similarly,
we could define some new functions to define computations related to
the Point class:
import math
def distance_to_origin(pt):
return (pt.x**2 + pt.y**2)**0.5
def euclidean_distance(pt1, pt2):
return ((pt1.x - pt2.x)**2 + (pt1.y - pt2.y)**2)**0.5
def manhattan_distance(pt1, pt2):
return abs(pt1.x - pt2.x) + abs(pt1.y - pt2.y)
def add_vectors(pt1, pt2):
new_pt = Point()
new_pt.x = pt1.x + pt2.x
new_pt.y = pt1.y + pt2.y
return new_pt
def angle_between(pt1, pt2):
vert = pt2.y - pt1.y
horiz = pt2.x - pt1.x
return math.atan2(vert, horiz)
However, just from looking at a program written in that style, it is
not obvious that there is any connection between the functions we've
defined, and the types of data they operate on. With some examination,
however, it becomes apparent that all of the operations above take
at least one instance of Point as an argument.
This observation is the motivation for methods. A method is a function that is associated with a particular class. Methods are semantically the same as functions, but there are two syntactic differences:
- Methods are defined inside a class definition in order to make the relationship between the class and the method explicit.
- The syntax for invoking a method is different from the syntax for calling a function.
Let's start by transforming one of these functions into a method. As a first step, all we have to do is to move the definition into the class (notice the change in indentation):
class Point:
n = 2
def distance_to_origin(pt):
return (pt.x**2 + pt.y**2)**0.5
Once we have defined distance_to_origin this way, we now have two
ways to call it. The first might seem familiar: if we have an
instance p of point, we can look up the function with
Point.distance_to_origin, and call it with p as an argument:
p = Point()
p.x = 3.0
p.y = 4.0
print(Point.distance_to_origin(p)) # prints 5.0
Using this notation, Python first looks up the name Point. It then
looks up the name distance_to_origin inside that object, and calls
the resulting function with the instance p passed in as an argument.
It turns out that people very rarely call methods using this syntax. Rather, we tend to use a more concise notation for calling methods:
print(p.distance_to_origin()) # also prints 5.0
This might seem weird! We defined distance_to_origin to take a
single argument, but above, it seems not to be taking any! If this
seems strange, that's normal. What we have here is a bit of "syntactic sugar:"
syntax to make a common operation easier/sweeter to write.
In this slight shift of notation, distance_to_origin is still the
name of the method we want to call, and its argument p is still the
object the function acts on. Behind the scenes, though, if a method
is looked up from an instance instead of from a class, Python will
automatically insert that instance as the first argument to the method
(so in this case the instance p is associated with the name pt
inside the method body).
Note: In fact, we have seen this syntax before! When we used
append to add elements to the end of a list x, we did it by saying
x.append(elt). But it turns out that we could also have done
list.append(x, elt).
By convention, the first parameter of a method is called self, so it
would be more common to write distance_to_origin like this:
class Point:
n = 2
def distance_to_origin(self):
return (self.x**2 + self.y**2)**0.5
The reason for this convention is an implicit metaphor:
- The syntax for a function call,
distance_to_origin(pt), suggests that the function is the active agent. It says something like, "Heydistance_to_origin! Here's a point I want you to calculate the distance for." - In this new shift of perspective (often referred to as object-oriented programming), the objects are the active agents. A method invocation like
p.distance_to_originsays "Heyp! Please tell me your own distance to the origin."
This change in perspective might be more polite, but it is not obvious that it is useful. In the examples we have seen so far, it may not be. But sometimes shifting responsibility from the functions onto the objects makes it possible to write more versatile functions (or methods), and makes it easier to maintain and reuse code.
5.1) What is self?
In this section, we'll expand a bit more on self (in Python, not philosophically!).
First, it's important to note that self is just a name, which is
typically used as the first parameter to a method. This first
argument, regardless of what it is called, always denotes the
instance that is currently being operated on.
If a method is looked up via a class, it is up to the programmer
to provide the instance of that class that the method should act on.
If the method is looked up via an instance, however, Python will
automatically insert that instance as the first argument to the method
(the argument typically called self).
Let's expand on the definition of Point from above to include one
more method, and then invoking a couple of methods:
class Point:
n = 2
def distance_to_origin(self):
return (self.x**2 + self.y**2)**0.5
def euclidean_distance(self, other):
return ((self.x - other.x)**2 + (self.y - other.y)**2)**0.5
p1 = Point()
p1.x = 3.0
p1.y = 4.0
p2 = Point()
p2.x = 7.0
p2.y = 8.0
print(p1.distance_to_origin())
print(p2.euclidean_distance(p1))
Modify the Point definition to convert the other functions from
above (angle_between, manhattan_distance, add_vectors) to
methods. How would you call these methods from an instance p of
Point?
One reason self is useful is because it allows us to access and
modify attributes from within a method. Whereas variables defined
within a function are only accessible from that local frame,
attributes defined inside of self will be accessible from other
method calls, and, indeed, from outside the object!
This is important for objects with values unique to a particular instance across function calls (such as the Point class with x and y; or the Rectangle class with corner, height, and width).
6) The init Method
In the previous examples, it was kind of a pain to make new instances of the classes we've defined; we had to first make the instance, and then bind new variables inside the resulting object.
The init method (short for "initialization") provides a means for
easing this process. It is a special method that gets invoked when an
object is instantiated. Its full name is __init__ (two
underscore characters, followed by init, and then two more
underscores). An init method for the Point class might look like
this:
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
Once we have defined this method, we can create an instance like so:
mypoint = Point(2, 3)
If arguments are passed in when creating an instance of a class,
Python will pass them to the class's __init__ method. In
particular, Python will do the following in response to the code
above:
- Create a new instance of
Pointand bind it to the namemypoint. - Run the
__init__method withmypointpassed in as the first argument (in the example above,Point.__init__(mypoint, 2, 3)). - Inside of the body of the function, the name
selfrefers to this new instance, so the function will store values2and3asxandy, respectively, inside the instance (so that they are accessible from outside the function asmypoint.xandmypoint.y).
It is common for the parameters of __init__ to have the same names
as the attributes. The statement:
self.x = x
stores the value of the parameter x as an attribute of self (the
newly-created instance).
7) Some Other "Magic" Methods
Python also has a number of other "magic" methods, which are called automatically by Python in certain situations, and which are typically denoted with a name surrounded by double-underscores. A more complete list is available here, but the following are a few examples:
__str__(self)should return a string; this method is called when the instance in question is printed, or when converting to a string with thestrfunction.__add__(self, other)is called when the+operator is used on two instances, allowing us to use the+operator on instances of our custom classes.__mul__(self, other)is called when the*operator is used on two instances.
As an example, consider printing one of the Point instances. Python will try its best to print a useful summary of the object, but the best it can do is something like:
p = Point(2, 3)
print(p) # prints: <__main__.Point object at 0x7f8d7fae9d68>
Not very helpful at all! But if we define a __str__ method first, we can get much nicer results:
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def __str__(self):
return "Point(" + str(self.x) + ", " + str(self.y) + ")"
p = Point(8, 4)
print(p) # prints: Point(8, 4)
Earlier on, when we were talking about different representations for points, we listed three possibilities:
- storing
xandyseparately as two variables, - storing coordinates in a list or tuple, or
- creating a new type to represent points as objects.
What are the benefits and drawbacks of each of these representations?
Any of these representations could, in fact, work fine, but the representation of a point using a class has a number of nice features:
- It is easy to make multiple instances of the
Pointclass, which would not be true of simply storing thexandycoordinates separately. - Creating the
Pointclass allows us to associate a number of methods specific to points with the objects themselves, rather than having them as separate stand-alone functions (which we would need if we were representing points as lists or tuples).
8) Extra Goodies
Now we switch to explaining some extra Python features. Ironically, one of the goals for this course has been to teach you as little Python as possible, in the sense that we wanted to focus on accurately modeling a small number of Python's features which are not unique to Python, and to provide a foundation on which future pieces can be added with relative ease.
Now we will go back for some of the good, relatively Python-specific bits that got left behind. Python provides a lot of features that are not really necessary (you can write good code to solve any problem without them), but with them you can sometimes write code that's more concise, readable, or efficient. You may have already seen many of these. We will now take the time to introduce them formally.
In this one section, there is not time to cover everything, but you will have plenty of time as you continue on with programming to pick up more and more of these little pieces!
8.1) "any" and "all"
Python provides a built-in function, any, that takes a sequence of
boolean values and returns True if any of the values are True. It
works on lists:
print(any([False, False, True])) # True
But it is often used with expressions like this:
print(any(letter == 't' for letter in 'monty')) # True
That example isn't very useful because it does the same thing as the
in operator. But we could use any to rewrite more complicated
behaviors. For example, consider the following function:
def avoids(word, forbidden):
for letter in word:
if letter in forbidden:
return False
return True
We could have rewritten this function using any:
def avoids(word, forbidden):
return not any(letter in forbidden for letter in word)
The function almost reads like English: "word avoids forbidden if
there are not any forbidden letters in word."
Using any with a generator expression is efficient because
it stops immediately if it finds a True value,
so it doesn't have to evaluate the whole sequence.
Python provides another built-in function, all, that returns
True if every element of the sequence is True. For example:
print(all([False, False, True])) # False
nums = [2, 4, 6]
print(all(num % 2 == 0 for num in nums)) # True
8.2) Multiple Inline Comparisons
Earlier, we talked about Python's comparison operators (>, <,
>=, <=, ==, !=) as though they were binary operators, but it
turns out that these are actually n-ary (that is, they can take more
than 2 operands).
For example, we could write:
x < y < z
which will evaluate to True only if x is less than y and y
is less than z. This also works for the other comparators (and even
for combinations of different comparators).
For example:
a == b == c # evaluates to True if a == b and b == c
a > b < c # evaluates to True if a > b and b < c
8.3) Error Handling
At some point when working on the exercises in this class, you may have encountered errors that were difficult to predict. In these cases, it would be nice to have a way for Python to detect that an error (in Python speak, an exception because it is not normal behavior) occurred, and to behave appropriately.
In some cases, rather than trying to predict errors, it is better to
go ahead and try (and deal with problems if they happen), which is
exactly what the try statement does. The syntax is similar to an
if...else statement:
def safe_divide(x, y):
try:
return x / y # this could result in a 'divide by zero' error
except:
print("Error in division!")
return None
Python starts by executing the try body. If all goes well, it skips
the except clause and proceeds. If an exception occurs, it jumps out
of the try clause and runs the except clause.
Handling an exception with a try statement is called "catching" an
exception. In this example, the except clause prints an error message
that is not very helpful. In general, catching an exception gives you
a chance to fix the problem, or try again, or at least end the program
gracefully (rather than with a spew of Python-related red text).
9) Defining Functions - Lambda Notation
We've seen one line if/else statements and one line for loops, so you may be
wondering if there are other one-line short cuts? Turns out the answer is yes!
One "one-liner" that is sometimes useful is the lambda keyword, a convenient
new way to define functions.
The most common way to define functions in Python, which we've already seen, is via the def keyword. For
example, earlier we made a function that doubled its input, like so:
def double(x):
return 2*x
Recall that this will make a new function object in memory, and associate the name
double with that object.
Python has another way of defining functions: the lambda
keyword2. The below expression is also a function that doubles its input:
lambda x: 2*x
The variable name(s) before the colon, here just x, are the names of the arguments. The
expression after the colon is what the function will return.
This function is almost exactly the same as double,
except that it does not have a name.
We could have used a lambda instead of a def when
creating the response for double from above:
def response(f, lo, hi, step):
out = []
i = lo
while i <= hi:
out.append(f(i)) # here, we apply the provided function to i
i += step
return out
double_out = response(lambda x: 2*x, 0, 1, 0.1)
If we did not care about being able to access double outside of
computing its response, it might make sense to do this. This is the same as
passing a function in as the first argument to response; the
function is just being defined with lambda instead of with
def.
We could do the same to get the response for square:
square_out = response(lambda x: x**2, 0, 1, 0.1)
And we could have defined add_n as follows:
def add_n(n):
return lambda x: x+n
You can also define functions of more than one argument using lambdas. Both of the below pieces of code define multiply to be a function which returns the multiplication of its two inputs, for example:
def multiply(a, b):
return a*b
multiply = lambda a, b: a*b
You should know that lambda, while sometimes a nice convenience, is never necessary—you
can always use def instead! Similar to the list comprehension syntax we'll explore below in section 6, the lambda syntax is less explicit about what Python is doing than its def counterpart, and it's harder to debug since it cannot include print statements. As such, use it sparingly, and only when the function body is simple (e.g., a one-line return statement).
9.1) Enumerate
Have you ever wanted to both index and get the element from a list? Well
Python has an enumerate function that will do just that.3
seasons = ['Spring', 'Summer', 'Fall', 'Winter']
for i in range(len(seasons)):
season = seasons[i]
print(i, season)
# can be written more succinctly with enumerate:
for i, season in enumerate(seasons):
print(i, season)
print(list(enumerate(seasons)))
# [(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]
enumerate can take any iterable as an argument (anything that can be looped over!)
9.2) Zip
Have you ever wanted to get the corresponding elements from separate lists?
Well Python's zip function that will do just that.
first = ['Tim', 'Duane', 'Hope', 'Jeff']
last = ['Beaver', 'Boning', 'Dargan',]
smaller = min(len(first), len(last))
for i in range(smaller):
fname = first[i]
lname = last[i]
print(fname, lname)
# with zip:
for fname, lname in zip(first, last):
print(fname, lname)
print(list(zip(first, last))) # [('Tim', 'Beaver'), ('Duane', 'Boning'), ('Hope', 'Dargan')]
zip will take any number of iterable (loopable) arguments and produce tuples
of the corresponding elements in order (cutting off at the end of the shortest argument). You can read more about zip and other built-in functions by reviewing Python's
documentation here.
10) Python Goodies Review
While prior readings have covered these topics, the following sections offer some review that may be helpful:
10.1) Sequence Unpacking
It is often useful to swap the values of two variables. With
conventional assignments, you have to use a temporary
variable. For example, to swap a and b:
temp = a
a = b
b = temp
This solution is cumbersome; tuple assignment is more elegant:
a, b = b, a
The left side is a tuple of variables; the right side is a tuple of expressions. Each value is assigned to its respective variable. All the expressions on the right side are evaluated before any of the assignments.
The number of variables on the left and the number of values on the right have to be the same:
a, b = 1, 2, 3 # this produces: ValueError: too many values to unpack
This error message might seem weird, but this idea of assigning each element in a sequence to a different variable name is often referred to as unpacking that sequence.
For example, consider the following three pieces of code to compute
the distance between points (where points are represented as (x, y)
tuples.
def distance(pt1, pt2):
return ((pt1[0] - pt2[0])**2 + (pt1[1] - pt2[1])**2)**0.5
def distance(pt1, pt2):
x1 = pt1[0]
y1 = pt1[1]
x2 = pt2[0]
y2 = pt2[1]
return ((x1 - x2)**2 + (y1 - y2)**2)**0.5
def distance(pt1, pt2):
x1, y1 = pt1
x2, y2 = pt2
return ((x1 - x2)**2 + (y1 - y2)**2)**0.5
The first function definition is nice and to-the-point, but it is a bit hard to read because the indexing operations are all collapsed together with the mathematical operation to compute the distance. The second makes the last line easier to read, but at the expense of having to write 4 extra lines of code. The last, I think, strikes a nice balance between the two.
More generally, the right side can be any kind of sequence (string, list or tuple). For example, to split an email address into its username and domain name, we could do:
address = 'a_clever_username@mit.edu'
uname, domain = address.split('@')
The return value from split is a list with two elements;
the first element is assigned to uname, the second to
domain.
print(uname) # prints a_clever_username
print(domain) # prints mit.edu
10.2) Generating Graphs with matplotlib
The matplotlib.pyplot module provides a number of useful functions for
creating plots with Python. In this section we'll go over a few examples of how to generate different plots.
To import the pyplot module, add the following to the top of your script:
import matplotlib.pyplot as plt
Once you have done so, you can make a new plot by calling plt.figure() with
no arguments. After that, you can use various functions to add data
to the figures. When you are ready, calling the plt.show() function with
no arguments will cause matplotlib to open windows displaying the resulting
graphs. You can also add a legend and/or a title to the plot, as well as
labels to the axes, as shown in the example below.
The following code will cause four windows to be displayed. Try
running the code below on your own machine to see the results. Notice that the
plt.show() function does not return until the plotting windows are closed.
import matplotlib.pyplot as plt
# here we plot a set of "y" values only; these are associated automatically
# with integer "x" values starting with 0.
plt.figure()
plt.plot([9, 4, 7, 6])
# if given two arguments, the first list/array will be used as the "x" values,
# and the second as the associated "y" values
plt.figure()
plt.plot([10, 9, 8, 7], [1, 2, 3, 4])
plt.grid() # this adds a background grid to the plot
# we can also create scatter plots. scatter plots require both "x" and "y"
# values.
plt.figure()
plt.scatter([10,25, 37, 42], [12, 28, 5, 37])
# multiple calls to plt.plot or plt.scatter will operate on the same axes
plt.figure()
plt.scatter([10, 25, 37, 42], [12, 28, 5, 37], label='scatter')
plt.plot([10, 40], [5, 20], 'r', label='a line') # the 'r' means 'red'
plt.plot([5, 9, 15, 30], [10, 20, 30, 35], 'k', label='more data')
plt.title('A more complete example')
plt.xlabel('A label for x')
plt.ylabel('The vertical axis')
plt.legend()
# finally, display the results
print('Showing Graphs')
plt.show()
print('Done')
10.3) Slicing
You've seen before that it's possible to "index into" sequences (strings, lists, tuples) to extract particular values from them. It is also possible to select a segment (called a slice) of the sequence using a similar syntax.
Consider the following example using strings:
fruit = 'banana'
print(fruit[0:4]) # prints bana
print(fruit[2:4]) # prints na
The slicing operator [start:stop] returns the part of the string from the
start^\text{th}-indexed character to the stop-index character, including the
first but excluding the last.
If you omit the first index (before the colon), the slice starts at the beginning of the string. If you omit the second index, the slice goes to the end of the string:
print(fruit[:3]) # prints ban
print(fruit[3:]) # prints ana
If the first index is greater than or equal to the second the result is an empty string, represented by two quotation marks:
print(fruit[3:3]) # this results in the empty string `''`
An empty string contains no characters and has length 0, but other than that, it is the same as any other string.
Continuing this example, what do you think fruit[:] means? Try it
and see.
The slicing operator (similarly to the range function) also takes an
optional third argument (commonly referred to as step), which
specifies how many characters to 'skip' on each step. If it is not specified,
this value defaults to 1.
In its full form, this operator looks like [start:stop:step]. For example:
print(fruit[::2]) # bnn
print(fruit[0:4:3]) # ba
print(fruit[1::3]) # an
These numbers can sometimes be a bit confusing; it helps to think about this operator in terms of how it would be defined as a function:
def slice(string, start, stop, step):
out = ''
index = start
while index < stop:
out += string[index]
index += step
return out
Notice that step can be negative, which gives us an easy way to make a reversed version of a given sequence:
print(fruit[::-1])
The slice operator also works on lists:
t = ['a', 'b', 'c', 'd', 'e', 'f']
print(t[1:3]) # ['b', 'c']
print(t[:4]) # ['a', 'b', 'c', 'd']
print(t[3:]) # ['d', 'e', 'f']
If you omit the first index, the slice starts at the beginning. If you omit the second, the slice goes to the end. So if you omit both, the slice is a copy of the whole list.
print(t[:]) # ['a', 'b', 'c', 'd', 'e', 'f'] (but this is a DIFFERENT list containing the same elements)
Since lists are mutable, it can sometimes be useful to make a copy before performing operations that modify lists.
A slice operator on the left side of an assignment can update multiple elements:
t = ['a', 'b', 'c', 'd', 'e', 'f']
t[1:3] = ['x', 'y']
print(t) # ['a', 'x', 'y', 'd', 'e', 'f']
10.4) Optional Arguments to Functions
When defining a function, one sometimes want to be able to call the function with a particular argument, but also without it. For this, there are optional arguments. Consider this example:
def approximately_equal(x, y, threshold=0.1):
return abs(x - y) <= threshold
If threshold is specified (e.g., approximately_equal(x, y, 1e-6)),
then that value will be used for threshold (in this case,
10^{-6}). If not (e.g., approximately_equal(x, y)), then the
default value (0.1) will be used for threshold.
In other words, if we provide the optional argument, it overrides the default value.
If a function has both required and optional parameters, all the required parameters have to come first, followed by the optional ones.
There is a small caveat here (and often a big source of bugs): default values are evaluated at the time the function is defined, not when the function is called. So we have to be careful when using a mutable object as a default value for a parameter; if we do this, all calls to the function will use that same object (which may have been modified by previous calls).
10.5) Filtering List Comprehensions
Earlier, we saw how to use the concise list comprehension syntax to create a list based on another sequence. List comprehensions can also be used for filtering.
For example, if we had a list and we wanted to find the squares of the odd numbers in that list, we could do:
def squared_odd_numbers(input_list):
out = []
for i in input_list:
if i % 2 == 1: # if i is odd
out.append(i ** 2)
return out
or, using a list comprehension:
def squared_odd_numbers(input_list):
return [i**2 for i in input_list if i % 2 == 1]
This functions selects only the elements from input_list that are
odd, squares them, and returns a new list containing the result.
10.6) Ternary Conditional Expressions
You may want to set a variable to one thing if a certain condition is true, and another otherwise:
if my_condition:
x = a
else:
x = b
This is a lot of lines for a simple task. It turns out you can write the above like so:
x = a if my_condition else b
The expression on the right hand side evaluates to a if my_condition is True;
otherwise, it evaluates to b. The overall statement is an assignment statement,
so that a or b is assigned to the variable x.
11) Summary
In this set of readings, we first learned about a powerful new feature of Python: classes, which allowed us to define new types of Python objects. Just as functions allowed us to abstract away details of particular operations and treat them as though they had been built in to Python, classes let us abstract away details of particular data types and treat them as though they were built in to Python.
Then we also shared a bunch of concise syntax features of Python.
Next Exercise: Things
Footnotes
1As a noun, "AT-trib-ute" is pronounced with emphasis on the first syllable, as opposed to "a-TRIB-ute", which is a verb.
2This may seem like a bizarre name, but it comes from a mathematical system for expressing computation, called the Lambda calculus.
3 The example below comes from Python's official documentation for enumerate
 6.s090
6.s090