Readings for Week 4

Licensing Information

The readings for 6.S090 are licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. You are free to make and share verbatim copies (or modified versions) under the terms of that license.

Portions of these readings were modified or copied verbatim from the very nice book Think Python 2e by Allen Downey.

PDF of these readings also available to download: reading4.pdf

Table of Contents

So far, we have learned about a number of useful tools in Python. We have learned about:

• several types of Python objects that allow us to represent a variety of things in Python's memory (the types we have seen so far include numbers, strings, Booleans, the special None value, and compound objects like lists, tuples, and dictionaries); and
• several control flow mechanisms that allow us control over the order in which statements in a Python program are executed (the control flow mechanisms we have seen so far include if/elif/else, and while and for loops).

These are some really powerful tools, and, as you've seen through the exercises, they are enough to accomplish a wide variety of things!¹ However, this week, we'll learn about an incredibly powerful means of abstraction that will help you manage the complexity as the programs you write become more and more complicated: functions.

Let's start our discussion of functions by considering the following code, which is designed to compute the result of evaluating a polynomial (represented as a list of coefficients) at a particular numerical value:

coeffs = [7, 9, 2, 3] # represents 7 + 9x + 2x^2 + 3x^3
x = 4.2

result = 0
for index in range(len(coeffs)):
   result = result + coeffs[index] * x ** index
print(result)

This is a nice piece of code in the context of a program that requires evaluating a polynomial, but in some sense it isn't as useful as it could be, in that it works only for the values of coeffs and x given above.

It is possible, however, to imagine a larger program that requires evaluating several polynomials. With the tools we have available to us so far, if we wanted to use the code above to this end, we would have to copy the code and paste it to new locations several times.
Depending on what our program is doing, we might need to change the variable names coeffs, x, and result to prevent them from overwriting values we had computed for other polynomials. This is a pain! Not to mention, if we find a bug in our implementation, we would have to go back and fix it in every copy-pasted copy we made of this code!

It would be nice to be able to generalize the notion of this computation so that we could perform it on arbitrary inputs as part of a larger program. It turns out that a new type of Python object called a function, will allow us to do this!

Functions are arguably the most powerful tool any programmer can have in their toolkit, but it can be a bit complicated to keep track of how Python handles them. As such, we're going to introduce relatively few new topics in this section, so that we can focus on functions, on how Python goes about evaluating code inside a function, and on how they can be used to increase the modularity of the programs we write.

A function is a type of Python object that represents an abstract computation. It can help to think of a function as a little program unto itself, which performs a specific task. Internally, that's what a function really is: it is a generalized sequence of statements that Python can evaluate to compute a result. This is perhaps not the most elegant definition in the world, so let's move on by way of example.

Python comes with several functions built in, and, in fact, we have already seen several examples of functions in Python. For example, we already learned about len, which computes the length of an input sequence. We could use len inside of a program, for example, by evaluating the following expression: len("twine")

In this example, the name of the function we are working with is len. The parentheses indicate that we want to "call" the function², which means to evaluate the sequence of statements it represents. The expression inside the parentheses (here, "twine") is called an argument³ to the function. In this case, the result is an integer representing the length of the argument.

It is common to say that a function "takes" one or more arguments as input and "returns" a result. This result is also called the return value. In this case, len is a function object, and the result of calling it is an int. But, importantly, functions can return values of any type!⁴

We can treat the result of calling a function the same way we would treat any other Python object. For example, we could:

print(len("twine"))  # print the result
x = len("yarn")  # store the result in a variable
y = len("thread") + 27/2  # combine the result with other operations.

Multiple Arguments

Some functions take more than one argument. To specify this, we separate arguments with commas inside the parentheses associated with a function call. For example, consider Python's built-in divmod function, which takes two arguments:

print(divmod(19, 4))   # divmod returns a tuple; this will print (4, 3)

Alternate Forms of Previous Functions

It turns out that two of the functions we have already dealt with have alternate forms that take more than one argument, which may be useful in your programs moving forward:

• If print is given more than one argument, it will print all of its arguments on the same line, separated by spaces. If it is given no arguments (i.e., print()), it will simply make a blank line.
• range has three forms:

  • If range is given a single integer x, the object it returns contains the numbers from 0 to x-1, inclusive.

  • If range is given two integers x and y, the object it returns contains the numbers from x to y-1, inclusive.

  • If range is given three integers x, y, and z, the object it returns contains all values x + i\times z such that x \leq x + i\times z \lt y, in increasing order of i. We can think of z as the step size that we take to go from x to y. This form is commonly used to iterate backwards: range(10, 0, -1).

x = print(7)
print(x)

print(print(print(10)))

10
None
None

Substitution Model

Before we can go too much farther, we need to think about how Python evaluates functions in our substitution model. In order to evaluate a function call, Python takes the following steps:

• Looks up the value to the left of the parentheses
• Evaluates each of the arguments from left to right
• Calls the function with the results of evaluating the arguments

divmod(17 + 2.0, len("ca" + "ts"))

divmod(19.0, len("ca" + "ts"))

divmod(19.0, len("cats"))

divmod(19.0, 4)

(4.0, 3.0)

x = 2
z = x(3.0 + 4.0)
print(z)

Using built-in functions or functions imported from Python modules is all well and good, but real power comes from being able to define functions of your own. This is accomplished via a new kind of Python statement called a function definition statement, which uses a Python keyword called def.⁵

This is perhaps best seen by example:

def maximum(x, y):
  if x > y:
    z = x
  else:
    z = y
  return z

This statement does two things:

• it creates a new function object in memory, and
• it associates the name maximum with that object in the current frame.

A function definition statement always starts with the keyword def, followed by an arbitrary name for the function. The sequence of names within the parentheses after the function's name are called parameters or, interchangeably, arguments (in this case, x and y), and the function describes a computation in terms of those parameters (as well as, potentially, other values, constants, etc).

Like many of the structures we have seen, function definitions also have a body (all the code that is indented one level farther than def; in this case, the whole if/else statement). The return keyword, which is only usable inside a function definition, tells Python what the function should produce as its return value when it is called.

Importantly, this statement only defines the function; Python does not run the code in the function body yet! It simply makes an object that represents this function and associates the given name with that object.

As with every new object we've introduced, we'll need a way to represent these objects in memory. Functions need to keep track of three pieces of information, and we'll try to depict all of those in our representation:

1. The names of the parameters to the function, in order;
2. The code in the body of the function; and
3. The frame in which the function was defined.

The following shows an example environment diagram that would result after executing the function definition statement above:

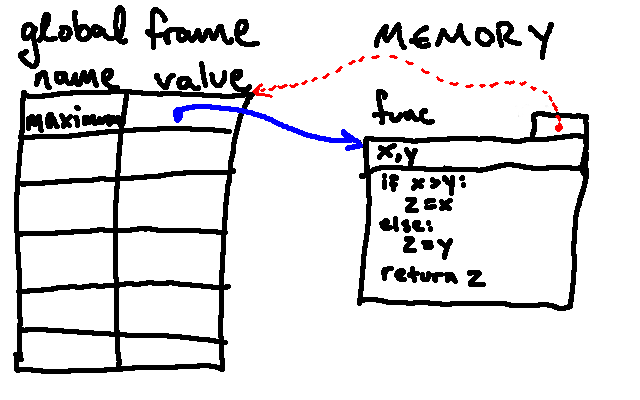
A few notes about this drawing:

• Note that the function definition did two things: it created a new function object, and it bound the name maximum to that object in the global frame.
• The names x,y on the top line of the function object represent the parameters of the function.
• The red arrow points back to the frame in which the function was originally defined (in this case, the global frame).

We can then call this function just as we would with any of the built-in functions (or imported functions) we've seen so far. For example:

a = 7.0
b = 8.0
x = 3.0
y = 4.0

c = maximum(a, b)

We'll now spend some time learning about what happens when this function is called. In the simplest terms, this is what happens:

1. First, Python looks up the name maximum and finds the function object in memory.
2. Next, Python runs the code in the function body with the parameters replaced with the values given (here, the body of the function would be evaluated with x replaced by 7.0 and y replaced by 8.0) until either a return statement or the end of the body is reached. If a return statement was reached, execution of the function stops and the associated value is returned; if the end of the function was reached (without hitting a return statement), the function returns None.

So after running the code above, c will have value 8.0.

That said, it will be important for us to understand how exactly Python got to that result, and so we'll go into more detail on these steps in the next section. Grab a cup of tea and settle in! This will get complicated, but understanding it is crucial to understanding some of the behaviors we will see from Python in the future! Don't be afraid to re-read multiple times, and, of course, to ask questions if you are confused!

We now examine what happens when a user-defined function is called. We'll go through the example from above. In next week's readings, we'll explore more complex examples.

Here is the code (repeated from above) for our example:

a = 7.0
b = 8.0
x = 3.0
y = 4.0

c = maximum(a, b)

(Assume that maximum has already been defined as above)

We know how the first four lines will behave: Python will associate the names a, b, x, and y with the values 7.0, 8.0, 3.0, and 4.0, respectively, in memory, resulting in the following environment diagram:

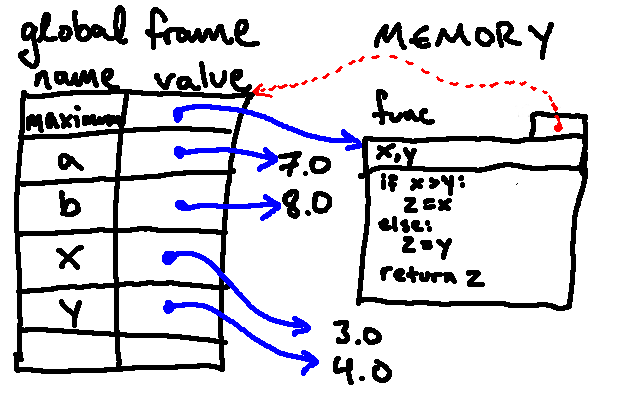
Now we are on to the line where the function call is evaluated. To accomplish this evaluation, Python completes the following steps:

1. As we saw with built-in functions, Python first starts by evaluating the name maximum (finding the function object), followed by the arguments to the function (which evaluate to the 7.0 and 8.0 that a and b, respectively, point to).

2. This is where things get different. Python's next step when calling a user-defined function is to create a new frame. This frame will be similar to the global frame in that it will map names to variables, but these variables will be local to the function (i.e. they will only be accessible inside the function being called).

   Once this new frame is created, Python binds the names of the parameters to the argument that were passed in to the function. From this point on, variable lookups will happen inside this new frame (until the function is done executing).

   This frame also contains a "parent pointer" to the environment in which the function being called was defined.⁶

   Once this step is done, we will have an environment diagram like the following:

   

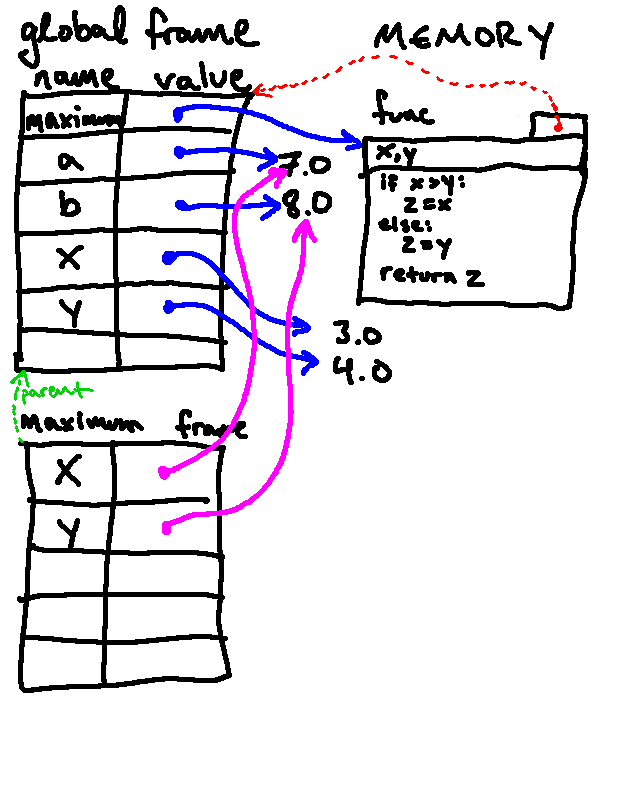
   As promised, this is a bit complicated. The frame in the bottom-left contains the bindings that exist inside the function. The green arrow represents the "parent pointer."

3. Python then executes the body of the function within this new frame. This means that, if Python looks up x, it finds the value 7.0 (bound in this frame), rather than the 3.0 value that is bound in the global frame. When looking up a variable, if it is not found in the current frame, Python then continues looking for that name in the parent frame before giving up.

   In the process of executing the function body, if Python makes any new assignments, those are also made in the current frame.

   So when our example code assigns a value to the variable z, that binding is made in the current frame. In the course of executing the conditional, we assign z to the same value as y, which results in the following environment diagram: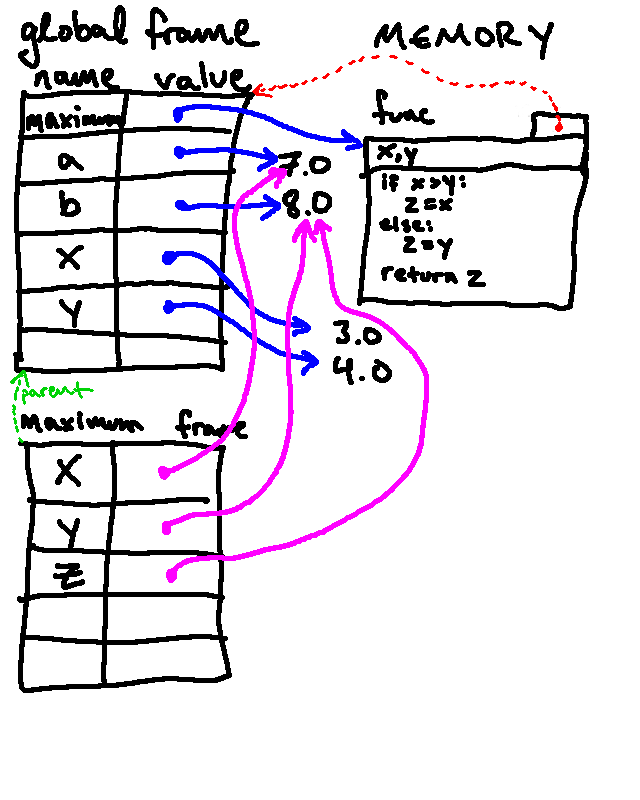

   

4. When the body is over or a return statement is reached, Python notes the value to be returned. (In the below diagram, the red "return" does not indicate an actual new variables called "return"; rather, it simply indicates the value that is to be returned from the function). Here, the return value was z, which pointed to the 8.0 currently in memory, so that is the value that will be available as the result of calling this function: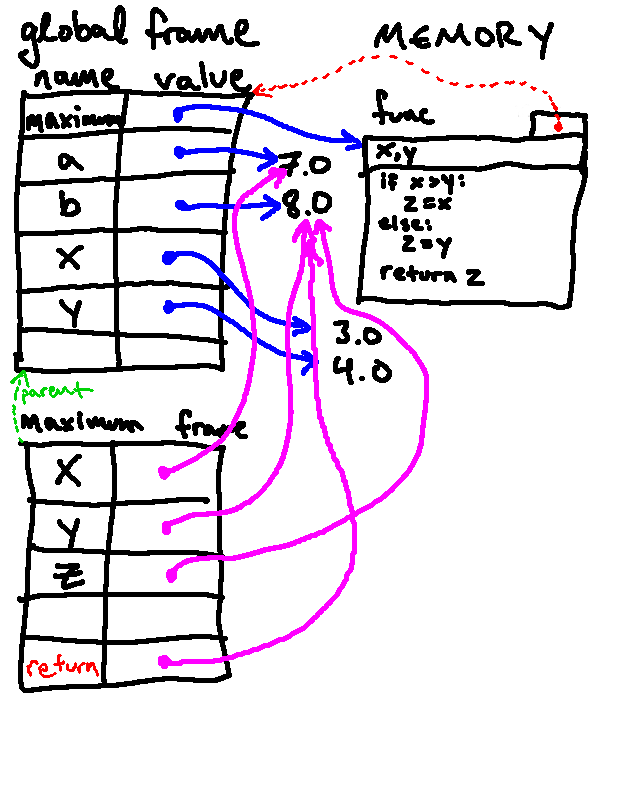

   

   Python then stops executing this function and returns to executing in the frame from which the function was called, after returning the value in question. It also cleans up the new frame it created⁷. In our example from above, the return value is then associated with the name c in the global frame, leaving us with the following: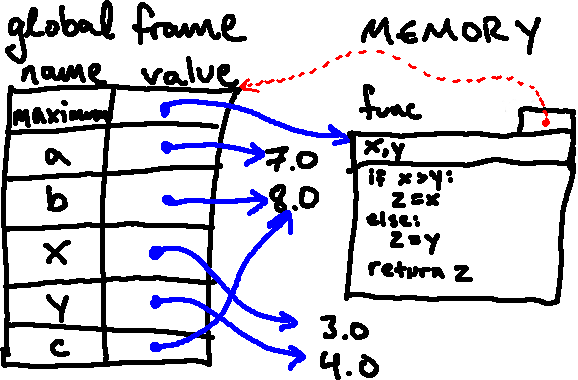

   

Abstraction

Notice that above, the process of creating the new frame gave us a wonderful feature: the variables inside the function body don't affect the variables outside the function body. This allowed us to call something x inside the function body and not have that cause problems with the thing called x outside the function (when the function is done executing, if we print x, we see the 3.0 that was assigned to x in the global frame)!

This is the real reason functions are so powerful: they offer us a means of abstraction (meaning, once we have defined a function, we can use it knowing only its end-to-end behavior, without worrying about exactly how that behavior was implemented in the function body, what variable names were used, etc).

Short Version

Here is the short version of Python's process for calling a user-defined function (again, for details, please see above):

1. Evaluate the arguments. (If an argument is itself a function call, apply these steps to it.)
2. Make a new frame. It stores a pointer to the frame's parent (the frame in which the function was defined).
3. Bind the arguments. In step 1, you already evaluated and simplified the arguments. Now you just have to bind variables to those values in the new frame.
4. Execute the body of the function in this new frame. Depending on what you see, you may be drawing more bindings and/or drawing new frames.
5. Note the return value of the function.
6. When execution has finished, remove the frame and resume execution in the calling frame.

Now that we have talked about the notion of multiple frames, we can clear something up about Python's built-ins. We have talked a lot now about how Python looks up the values associated with variable names, and you may have wondered how Python found the built-in values.

How did Python know what function to call when we referenced print? It is true that print and the other built-ins do not exist in the global frame. Rather, we can think of the global frame itself as having a parent pointer to a special "built-ins" frame: when Python looks up a name in the global frame and doesn't find it, it then looks in this special "built-ins" frame before throwing a NameError.

This is how the lookups for, for example, print and len proceed: Python first looks for them in the global frame. Since it doesn't find them there, it looks in the built-ins frame, where it finds them.

Failed variable lookups also proceed in this same way. Say we made a typo and were accidentally looking up the value pritn. In looking this up, Python would first look in the global frame; when it doesn't find pritn there, it would then look in the built-ins frame; and when it doesn't find pritn there either, it will give up and raise a NameError.

We close with some motivation for using functions, which should now be more clear:

• Creating a new function gives you an opportunity to name a group of statements, which makes your program easier to read and debug.
• Functions can make a program smaller by eliminating repetitive code. Later, if you make a change, you only have to make it in one place.
• Dividing a long program into functions allows you to debug the parts one at a time and then assemble them into a working whole.
• Well-designed functions are often useful for many programs. Once you write and debug one, you can reuse it.

In this reading, we (mainly) introduced functions. Importantly, we also talked about defining new functions of your own creation as a means of abstracting away details of a particular computation so that it can be reused. We spent a good deal of time and effort focusing on how defining and calling these functions fits in to our mental models of Python (substitution model and environment diagrams). Next week we'll solidify this understanding of functions further, with more examples, and we'll introduce some more related function features.

In this set of exercises, you will get practice with simulating the evaluation of functions and with defining functions of your own.

Before closing fully, we briefly describe some of Python's "syntactic sugar" to which you've been exposed. Wikipedia explains that syntactic sugar is "syntax ... that is designed to make things easier to read or to express. It makes the language 'sweeter' for human use: things can be expressed more clearly, more concisely, or in an alternative style that some may prefer."

List Comprehensions

In previous weeks, we've seen a common pattern related to creating a list of elements based on another sequence. For example, this function takes a list of strings and returns a new list of strings with an "s" added to each:

def add_s_to_all(words):
    res = []
    for word in words:
        res.append(word + "s")
    return res

We can write this more concisely using a list comprehension:

def add_s_to_all(words):
    return [word + "s" for word in words]

You can almost read the code like English, but here's what this means:

• The square brackets indicate that we are constructing a new list.
• The first expression inside the brackets (word + "s") specifies the elements of the new list.
• The for clause indicates what sequence (the words list) we are traversing.

The syntax of a list comprehension is a little awkward because the loop variable, word in this example, appears in the expression before we get to the definition.

You can also use this syntax to construct lists from other sequences, e.g. dictionaries. This function takes a dictionary and returns a new list containing all its values:

def list_of_values(d):
    res = []
    for key in d:
        res.append(d[key])
    return res

You have already seen a few other ways you could write this function:

def list_of_values(d):
    res = []
    for value in d.values(): # iterate over the values explicitly
        res.append(value)
    return res

def list_of_values(d):
    return list(d.values()) # get the values and make them into a list

You could also rewrite it using a list comprehension, either of these ways:

def list_of_values(d):
    return [d[key] for key in d]

def list_of_values(d):
    return [value for value in d.values()]

Compare these two to the above functions. Again, the square brackets indicate the creation of a new list, the first expression in the square brackets describes what elements to add to the list, and the for clause indicates what sequence to traverse.

Summing

In previous weeks, we've also seen a common pattern related to summing some values based on a sequence. For example, this function takes a list of positive numbers and returns the sum of their square roots⁸:

def sum_of_roots(nums):
    # make a list of the things to sum
    roots = []
    for num in nums:
        roots.append(num**0.5)

    # now sum them
    total = 0
    for root in roots:
      total += root

    return total

First of all, we can leverage Python's sum function to compress the second part of the computation:

def sum_of_roots(nums):
    roots = []
    for num in nums:
        roots.append(num**0.5)

    return sum(roots) # sum takes a list and returns the sum of its elements

As seen before, we could also create the roots list using a list comprehension:

def sum_of_roots(nums):
    roots = [num**0.5 for num in nums]
    return sum(roots)

Now, we can eliminate the temporary roots variable, and pass the list we want to sum directly into the sum function:

def sum_of_roots(nums):
    return sum([num**0.5 for num in nums])

And, as a final syntactic improvement, it turns out that we don't need to explicitly create a list to pass to the sum function. sum is in fact able to take in the bracketless expression num**0.5 for num in nums, too. (Recall that the square brackets around that expression were what indicated that we were forming a new list⁹.) So you may also see syntax like this:

def sum_of_roots(nums):
    return sum(num**0.5 for num in nums)

Notes

Importantly, you can always write your code using conventional syntax (using explicit for loops) instead of the syntactic sugar shown in this section. Conventional syntax is more explicit—it makes it clearer what exactly Python is doing. And it's also easier to debug, since you can't put a print statement inside the loop of a comprehension. We therefore recommend using comprehensions sparingly in your own code, and mostly for computations that are relatively simple. Once you build familiarity with loops, you can experiment more with this syntax.

Next Exercise: Fun with Functions

Back to exercises