Efficient Packing

1) Preparation

The following file contains code and other resources you will need for this exercise: u5_alternate_packing.zip

All of your changes should be made to lab.py, which you will submit at the end of this exercise. Importantly, you should not add any imports to the file. As usual, we have also provided test.py for local testing.

2) Introduction

You and your quarantining family and friends decide to take a camping trip to a remote forest. When you arrive, you notice that the ground is incredibly rocky. Still, you're determined to make the most of the situation, and make use of as much of the floor space as possible in teh tent.

Your assignment is to find a way to pack the tent with sleeping bags such that: 1. No one is sleeping on a rock. 2. Every usable (non-rock) portion of the tent is being utilized. If no such arrangement exists, you must correctly conclude that no such packing exists.

Specifically, you will implement the function pack(tent_size, missing_squares), described more below.

3) Representing Tents and Friends

We will use a 2-dimensional grid to represent the tent. Each rock occupies one square in this grid. A tent configuration is described by the variables:

• tent_size, which is a Python tuple with two integers (width, height)—the dimensions of the tent in terms of number of columns and number of rows in the grid.

• missing_squares, which is a Python set (possibly empty) of the grid squares with rocks under them. Each square is represented as a tuple with two integers (x, y), the coordinates of the square. The square (0,0) is at the top-left corner, and the x and y axes extend to the right and down, respectively.

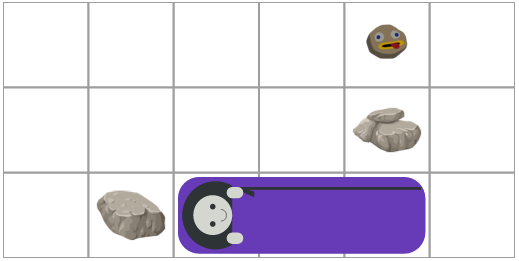
For example, a configuration would be represented as:

tent_size = (6, 3)
missing_squares = {(1, 2), (4, 0), (4, 1)}

This would denote the following tent configuration.

Each person requires a 3-by-1 block of space to sleep. Of course, this block can be oriented either vertically or horizontally. These blocks are represented by two parameters, anchor and orientation, where anchor denotes the top left square of the 3-by-1 block, and orientation is either 0 or 1, which corresponds to a horizontal or a vertical block, respectively.

For example, a person would be represented as a dictionary:

{
  "anchor": (2, 2),
  "orientation": 0
}

In the example tent above this would correspond to:

4) Valid Tiling

Let's say our tent has dimensions width by height. A valid tiling is a list of people (with anchor and orientation values) such that:

• For each square (i,j) occupied by a sleeping bag (three such squares per person):
  • 0 <= i < width and 0 <= j < height (i.e. each person lies entirely within the tent).
  • No rock exists under (i,j) (i.e. no person sleeps on a rock).
• No two 3-by-1 blocks have a square in common (i.e. no two people overlap).
• Every non-rock square is occupied by a person.

For example, let's say we are given the input from the above section:

tent_size = (6, 3)
missing_squares = {(1, 2), (4, 0), (4, 1)}

The following is a valid tiling for this tent with three horizontal and two vertical orientations.

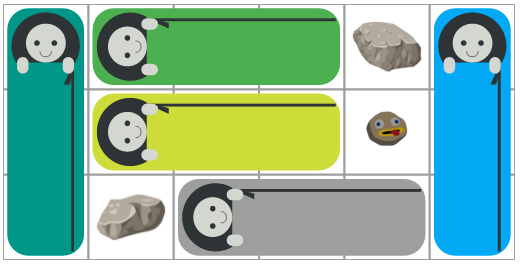
The corresponding list of people (in no particular order) would look like:

[
  {"anchor": (0, 0), "orientation": 1},
  {"anchor": (1, 0), "orientation": 0},
  {"anchor": (1, 1), "orientation": 0},
  {"anchor": (2, 2), "orientation": 0},
  {"anchor": (5, 0), "orientation": 1},
]

5) Suggested Approach

Since your solution must pass the test cases within the allotted time on the server, an approach which explores every single configuration of bags in the tent (i.e. tries every combination of placements of bags at every square of the tent) will not suffice. We describe one approach below. (You may attempt the problem on your own first if desired!)

As always, please free to ask for help!

6) Code Submission

Submit your lab.py below:

Please upload your code here. This question will be manually graded for correctness (% of test cases provided that pass in under 20 seconds) and good code style. Remember to use succinct, descriptive variable names, docstrings and comments to explain confusing lines.

Select File No file selected

Loading...

7) Applications

Although the particular application for this exercise was chosen in favor of accessibility and cute pictures, we hope you can see applications of the approach to other problems. The general algorithm, with perhaps some tweaks, could be applied to the following imaginative scenarios:

• You are tasked with tiling the floor of a newly constructed building. Your company only has tiles of a certain shape. You can cut the tiles into different, smaller shapes, but cutting is expensive. You want to determine an arrangement of the uncut tiles which leaves the least empty space (so that there are the fewest possible holes requiring cut tiles).
• You receive a large sheet of material. You can only sell material if it's cut into one of some certain shapes. You want cut the sheet to minimize the amount of it you waste (and maximize the amount of it that becomes part of a sellable shape).
• You have a model of the shapes and sizes of items you wish to pack into boxes for shipping. Shipping cost goes up with volume, since you have a limited number of trucks. You determine the most compact packing of the items.