Readings for Unit 3

Licensing Information

The readings for 6.S090 are licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. You are free to make and share verbatim copies (or modified versions) under the terms of that license.

Portions of these readings were modified or copied verbatim from Think Python 2e by Allen Downey.

PDF of these readings also available to download: 6s090_reading3.pdf

Table of Contents

1) Introduction

This week we're going to focus on learning about two new powerful built-in types: dictionaries and sets. Then we'll cover some new syntax that can help make our code more concise. Finally, we'll learn how to import and use a few packages in Python's extensive standard library, a collection of modules that can add functionality to your programs.

2) A Dictionary is a Mapping

First up: dictionaries. Dictionaries are one of Python's best features; they are the building blocks of many efficient and elegant programs. In some ways, a dictionary is like a list, but more general. Lists and dictionaries are both compound objects, and they are both mutable. In a list, though, the indices have to be integers, whereas in a dictionary they can be any hashable object.

A dictionary contains a collection of unique indices, which are called keys, and a collection of values. Each key is associated with a single value. The association of a key and a value is called a key-value pair or sometimes an item.

In mathematical language, we might say that a dictionary represents a mapping from keys to values, so you can also say that each key "maps to" a value. As an example, let's build a dictionary that maps from English to German words, so the keys and the values are all strings.

Lists in Python are created with square brackets (e.g., new_list = []). Dictionaries, on the other hand, are created with squiggly brackets. For example, we could make an empty dictionary with:

en_de = {}

To add items to the dictionary, you can use square brackets:

en_de['dog'] = 'Hund'

This line creates an item that maps from the key 'dog' to the value 'Hund'. If we print the dictionary now, we see a key-value pair with a colon between the key and value:

print(en_de)  # prints {'dog': 'Hund'}

This output format is also an input format. For example, you can create a new dictionary with three items:

en_de = {'dog': 'Hund', 'cat': 'Katze', 'guinea pig': 'Meerschweinchen'}

If you print en_de, you will see {'dog': 'Hund', 'cat': 'Katze', 'guinea pig': 'Meerschweinchen'}. ¹

To access a value in a dictionary, you can also use the square brackets:

print(en_de['cat'])  # prints Katze

If the key isn't in the dictionary, you get an error:

print(en_de['eagle'])  # gives us an error: KeyError: 'eagle'

So far, we've seen that square brackets are used to look up values in a dictionary, and also to add new items to a dictionary. It turns out that they are also used to change an existing mapping. For example, if we wanted our en_de dictionary to store the Swiss dialect German words, we could update our dictionary like so to account for this change:

en_de['dog'] = 'Hundli'
print(en_de)  # prints {'dog': 'Hundli', 'cat': 'Katze', 'guinea pig': 'Meerschweinchen'}

But we speak High German, so let's put it back:

en_de['dog'] = 'Hund'

2.1) Valid Keys and Values

Importantly, dictionaries are not limited to containing strings. They can have arbitrary objects as values, and arbitrary hashable objects as keys. An object is hashable if it has an unchanging hash value. You can determine whether an object is hashable by calling the hash function on it, which returns an integer. For example:

>>> hash(5)
5
>>> hash("hello")
-3280404559733277131
>>> hash(None)
-9223363241310935348
>>> hash(5.4)
922337203685478405
>>> hash((1,2,3))
529344067295497451

Calling the hash function on an unhashable object will raise an error:²

>>> hash([1,2,3])
    ...
TypeError: unhashable type: 'list'
>>> hash( ({1, 2}, 3))
    ...
TypeError: unhashable type: 'set'
>>> hash ({"hund": "dog"})
    ...
TypeError: unhashable type: 'dict'

Note that the hash value of an object can change between different runs of the same program. However, while a program is running, a hashable object will have a constant hash value. Additionally, objects that are equal (meaning object1 == object2 is True) will always have the same hash value.

In general, None and all ints, floats, booleans, and strings are hashable because they are immutable. Lists, dictionaries, and other mutable objects that can change are not hashable because their hash value is not guaranteed to be constant. Tuples are hashable only if all the elements inside the tuple are hashable (which is why ((1, 2), 3) is hashable but ([1, 2], 3) is not.)

Python implements dictionaries as a structure called a hash map. The details of this kind of structure are a bit beyond the scope of this class, but it is sufficient to know that the hash value of a key must be constant because that number is used to find the location in memory where the key's value is stored.

Note that you can mix-and-match different types of objects as the keys or values of a dictionary. While duplicate values are possible, keys are unique:

>>> d = {5: [1, 2, 3], "hi": [1, 2, 3], (1, 2): 3, (1, 2): 4}
>>> d
{5: [1, 2, 3], 'hi': [1, 2, 3], (1, 2): 4}

2.2) Dictionaries and Environment Diagrams

As we've done whenever we've introduced a new type of Python object, we'll learn a way to represent dictionaries in environment diagrams. Note that a dictionary is much like a frame in some ways; it is a mapping between keys and values. So our representation will look very similar: we'll put the keys in the left-hand side of this mapping, and the right-hand side will consist of pointers to the associated values.

For example, the following dictionary:

{'cow': "moo", 1: 2, (1, 2): [7, 8]}

would be represented as follows in an environment diagram:

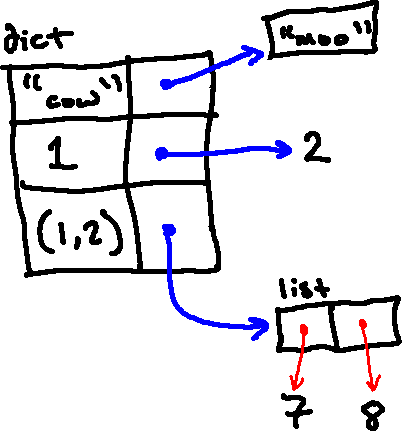
3) Other Dictionary Operations:

Beyond the operations above (adding, changing, and looking up key-value pairs), we can also do a number of other interesting operations on dictionaries.

3.1) Length

The len function works on dictionaries; it returns the number of key-value pairs:

>>> en_de = {'dog': 'Hund', 'cat': 'Katze', 'guinea pig': 'Meerschweinchen'}
>>> len(en_de)
3

3.2) Keys, Values, and Items

Sometimes instead of accessing a single value in a dictionary, we wish to access all the keys or all the values in a dictionary. Luckily, dictionaries have the keys(), values() and items() methods to do just that!

>>> en_de = {'dog': 'Hund', 'cat': 'Katze', 'guinea pig': 'Meerschweinchen'}
>>> en_de.keys()
dict_keys(['dog', 'cat', 'guinea pig'])
>>> en_de.values()
dict_values(['Hund', 'Katze', 'Meerschweinchen'])
>>> en_de.items()
dict_items([('dog', 'Hund'), ('cat', 'Katze'), ('guinea pig', 'Meerschweinchen')])

These methods return custom dictionary objects, but you can easily cast them to a list or a tuple as needed:

>>> list(en_de.keys())
['dog', 'cat', 'guinea pig']
>>> tuple(en_de.values())
('Hund', 'Katze', 'Meerschweinchen')
>>> list(en_de.items())
[('dog', 'Hund'), ('cat', 'Katze'), ('guinea pig', 'Meerschweinchen')]

3.3) Other Operations: The "in" Operator

Like we've seen with sequences, we can use the in operator to check whether something appears in a dictionary. By default, in will check whether a hashable value appears as a key in the dictionary, but we can also check whether any object appears as a value in the dictionary using the values method.

>>> 'cat' in en_de
True
>>> 'sandwich' not in en_de
True
>>> 'Katze' in en_de
False
>>> 'Katze' in en_de.values()
True
>>> [1, 2, 3] in en_de
    ...
TypeError: unhashable type: 'list'
>>> [1, 2, 3] in en_de.values()
False

4) Example: Dictionary as a Collection of Counters

Suppose you are given a string and you want to count how many times each letter appears. There are several ways you could do it:

1. You could create 26 variables, one for each letter of the alphabet. Then you could traverse the string and, for each character, increment the corresponding counter, probably using a chained conditional.

2. You could create a list with 26 elements. Then you could convert each character to a number, use the number as an index into the list, and increment the appropriate counter.

3. You could create a dictionary with characters as keys and counters as the corresponding values. The first time you see a character, you would add an item to the dictionary. After that you would increment the value of an existing item.

Each of these options performs the same computation, but each of them implements that computation in a different way.

An advantage of the dictionary implementation is that we don't have to know ahead of time which letters appear in the string and we only have to make room for the letters that do appear.

Here is what the code might look like:

def letter_count(string):
    '''
    Given a string, create a dictionary that counts the frequency of each character.
    '''
    d = {} # make a new dictionary
    for char in string:
        if char not in d:
            d[char] = 1 # we need to add the key to the d
        else:
            oldcount = d[char]
            d[char] = oldcount + 1 # key already exists in d, so increment its value
    return d

The first line of the function creates an empty dictionary d. The for loop traverses the string. Each time through the loop, if the character char is not in the dictionary, we create a new item with key char and the initial value 1 (since we have seen this character once). If char is already in the dictionary, we increment d[char].

If we printed the result of char_count('brontosaurus'), python would output:

{'a': 1, 'b': 1, 'o': 2, 'n': 1, 's': 2, 'r': 2, 'u': 2, 't': 1}

This indicates that the letters 'a' and 'b' appear once; 'o' appears twice, and so on.

4.1) Other Operations: "get"

The code above to check whether a key exists in a dictionary, and to use a default value (0 in the example above) if it does not, is a very common pattern. Because of this, Python provides an easier way to accomplish it: get.

To use get, you write it with a key and a default value. If the key appears in the dictionary, get returns the corresponding value; otherwise, it returns the default value. For example, working with our dictionary from earlier:

d = {'a': 1, 'b': 1, 'o': 2, 'n': 1, 's': 2, 'r': 2, 'u': 2, 't': 1}
print(d.get('a', 0))  # 1
print(d.get('p', 0))  # 0

string = "foo"
d = {}
for char in string:
    d[char] = d.get(char, 0) + 1
print(d)

5) Looping and Dictionaries

If you loop over a dictionary in a for statement, it traverses the keys of the dictionary by default. For example, we could print each key and corresponding value of a dictionary:

d = {'a': 1, 'b': 1, 'o': 2, 'n': 1, 's': 2, 'r': 2, 'u': 2, 't': 1}
for char in d:
    print(char, d[char])

and it will produce the following output:

a 1
b 1
o 2
n 1
s 2
r 2
u 2
t 1

This is equivalent to using the dictionary's built-in function .keys() which returns an iterable object with all of the keys:

for char in d.keys():
    print(char, d[char])

Again, you should generally not assume that the keys are in a particular order. To traverse the keys in sorted order, you can use the built-in function sorted:

for key in sorted(d):
    print(key, d[key])

produces the following output:

a 1
b 1
n 1
o 2
r 2
s 2
t 1
u 2

If your loop only uses the values in the dictionary, you can loop over the dictionary's .values():

for val in d.values():
    print(val) # prints the values

This is equivalent to the below:

for key in d:
    print(d[key])

You can also loop over both the keys and values at the same time, via .items():

for item in d.items():
    print(item) # prints a tuple (key, value)
    # can access the key via item[0]; the value via item[1]

You can also unpack this tuple of values into two separate variables:

for key, value in d.items():
    print((key, value))

This is equivalent to below:

for key in d:
    print((key, d[key]))

5.1) Example: Reverse Lookup

As we've seen, given a dictionary d and a key k, it is easy to find the corresponding value v = d[k]. This operation is called a lookup.

But what if you have a value v and you want to find k? You have two problems: first, there might be more than one key that maps to the value v. Depending on the application, you might be able to pick one, or you might have to make a list that contains all of them. Second, there is no simple syntax to do a reverse lookup; you have to search.

Here is code that prints all of the keys in d that map to a value v:

for k in d:
    if d[k] == v:
        print(k)

6) Sets

Sets can be thought of as similar to a collection of dictionary keys without values. Like dictionary keys, elements in a set are unordered, hashable, and unique.

Like dictionaries, we define sets using curly brackets:

>>> produce = {"tomatoes", "oranges", "bananas", "oranges"}
>>> produce
{'oranges', 'bananas', 'tomatoes'}

Displaying the value of produce in the python shell shows that sets have no duplicates and can shuffle the order of the original elements. Note that re-running this exact same code could produce different orderings of the elements.

We can also make an empty set and add elements to it:

>>> nums = set() # don't use {}, which will create an empty dictionary!
>>> nums.add(5)
>>> nums.add(5)
>>> nums.add(3)
>>> nums
{3, 5}

We can also convert any sequence of entirely hashable values to a set (and sets can be converted to a list, tuple, or string):

>>> set([1, 1, 2, 2, 3, 3])
{1, 2, 3}
>>> set(('my', 'favorite', 'tuple', 'my', ('inner', 'tuple')))
{('inner', 'tuple'), 'favorite', 'my', 'tuple'}
>>> set("hello")
{'l', 'h', 'o', 'e'}
>>> set(["good", ("fine",), (['uh oh'])])
    ...
TypeError: unhashable type: 'list'

Here are some methods we've seen before that also work on sets:

>>> nums = {4, 1, 1, 2, 4, 4}
>>> nums
{1, 2, 4}
>>> len(nums)
3
>>> 4 in nums
True
>>> 5 in nums
False

Note that determining whether something is in a set or dictionary is much faster than checking whether something is in a list, especially for large sequences.

However, unlike dictionaries and lists we cannot index into sets.

>>> nums[1]
    ...
TypeError: 'set' object is not subscriptable

But we can iterate over them:

for item in produce:
    print(item)
'''
Outputs:
bananas
tomatoes
oranges
'''

Additional operations can quickly determine the equality, intersection, difference, and union of sets:

>>> nums1 = {1, 2, 3}
>>> nums2 = {3, 4, 5}
>>> nums1 & nums2 # intersection: all elements that appear in both sets
{3}
>>> nums1 - nums2 # difference: all elements from first set that do not appear in second set
{1, 2}
>>> nums1 | nums2 # union: all elements from both sets combined
{1, 2, 3, 4, 5}
>>> nums1 == nums2 # equality: both sets contain the same elements
False

Note that [1, 2, 3] == [1, 3, 2] evaluates to False but set([1, 2, 3]) == set([1, 3, 2]) evaluates to True. This is because list equality cares about both the order and value of elements. Because sets are unordered the equality check just makes sure that both sets contain all the same elements.

6.1) Sets and Environment Diagrams

Sets can also mix-and-match and contain different hashable objects:

{1, "2", 3.4, False}

Because sets are unordered, we represent them as a blob with pointers to the values. We can represent the set above in an environment diagram as:

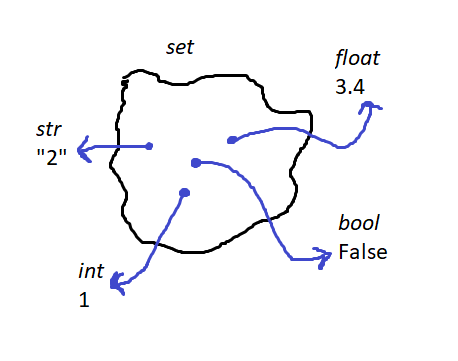
7) Ternary Statements

Now that we've learned about sets and dictionaries, let's take a moment to switch into a different gear: writing concise code. Python has provided some alternate syntax that can help make common operations that take a few lines of code only take a single line of code.

One example would be one-line if statements:

# print whether x is even or odd
x = 5
if x % 2 == 0:
    print("even")
else:
    print("odd")

# can also be written as
if x % 2 == 0:  print("even")
else: print("odd")

Note that this pattern should only be used when there is only a single line of code in the body of the conditional statement.

However, we can write this if / else statement even more concisely in one line as:

print("even" if x % 2 == 0 else "odd")

This is known as a ternary statement. Ternary statements have the pattern of TRUE_EXPRESSION if CONDITION else FALSE_EXPRESSION and can be used to make a four-line if / else statement into a single line, especially when it involves making a decision between two values.

Here's another example:

def positive_double(num):
    if num > 0:
        return num * 2
    else:
        return num * -2

def positive_double(num):
    return num * 2 if num > 0 else num * -2

print(positive_double(42))  # 84
print(positive_double(-5))  # 10

It's important to note that making code more concise does not necessarily make it better. Ternary statements can make the code harder to debug, and especially when it makes a single long line the code can become much less readable.

For example:

x = 5
y = 'This really long string that says x is positive' if x > 0 else 'A slightly different really long string that says x is not positive'

# this can be made slightly easier to read if you surround the statement
# with round brackets () and split it up over multiple lines
y = ('This really long string that says x is positive' if x > 0 else
      'A slightly different really long string that says x is not positive')

# but at this point it might be better to use a regular if/else so you
# can clearly see the conditional
if x > 0:
    y = 'This really long string that says x is positive'
else:
    y = 'A slightly different really long string that says x is not positive'

8) For Loop Comprehensions

Last week, we saw a common pattern related to creating a list of elements based on another sequence. For example, this function takes a list of strings and returns a new list of strings with an "s" added to each:

def add_s_to_all(words):
    res = []
    for word in words:
        res.append(word + "s")
    return res
print(add_s_to_all(["cake", "pie", "cookie"]))  # ["cakes", "pies", "cookies"]

We can write this more concisely using a list comprehension:

def add_s_to_all(words):
    return [word + "s" for word in words]

You can almost read the code like English, but here's what this means:

• The square brackets indicate that we are constructing a new list.
• The first expression inside the brackets (word + "s") specifies the elements of the new list.
• The for clause indicates what sequence (the words list) we are traversing.

The syntax of a list comprehension is a little awkward because the loop variable, word in this example, appears in the expression before we get to the definition.

You can also use this syntax to construct lists from other sequences, e.g., strings or tuples.

This function takes a string and returns a list containing all the letters in upper case:

def uppercase_list(word):
    return [letter.upper() for letter in word]

    # this list comprehension is equivalent to:
    result = []
    for letter in word:
      result.append(letter.upper())
    return result

    # or
    return list(word.upper())

print(uppercase_list('tomatoes')) # this prints ['T', 'O', 'M', 'A', 'T', 'O', 'E', 'S']

This function adds the index of an element to the number:

def add_index(nums):
    return [nums[i] + i for i in range(len(nums))]

    # equivalent to:
    result = []
    for i in range(len(nums)):
        result.append(nums[i] + i)
    return result

print(add_index([1,2,3,4])) # this prints [1, 3, 5, 7]
print(add_index((1,1,1,1))) # this prints [1, 2, 3, 4]

We can also use ternary statements inside list comprehensions. For example, this function takes a word and returns a list of letters in AlTeRnAtInG cAsE:

def alternating_case(word):
    return [(word[i].upper() if (i % 2) == 0 else word[i].lower())
                 for i in range(len(word))]

    # is equivalent to:
    result = []
    for i in range(len(word)):
        if (i % 2) == 0:
            result.append(word[i].upper())
        else:
            result.append(word[i].lower())
    return result

print(alternating_case('tomatoes'))
# this prints ['T', 'o', 'M', 'a', 'T', 'o', 'E', 's']
print(alternating_case('other_case'))
# this prints ['O', 't', 'H', 'e', 'R', '_', 'C', 'a', 'S', 'e']

An if statement at the end of a list comprehension filters what gets added to the new list. This function takes a list of numbers and returns a list with only even numbers:

def evens_only(nums):
    return [num for num in nums if num % 2 == 0]

    # this is equivalent to:
    result = []
    for num in nums:
        if num %2 == 0:
            result.append(num)
    return result

print(evens_only([1,2,3,4,8,7])) # this prints [2, 4, 8]

This function takes a dictionary and returns a new list containing all its values:

def list_of_values(d):
    res = []
    for key in d:
        res.append(d[key])
    return res

There are many other ways you could write this function:

def list_of_values(d):
    res = []
    for value in d.values(): # iterate over the values explicitly
        res.append(value)
    return res

def list_of_values(d):
    return list(d.values()) # get the values and make them into a list

You could also rewrite it using a list comprehension, either of these ways:

def list_of_values(d):
    return [d[key] for key in d]

def list_of_values(d):
    return [value for value in d.values()]

Compare these two to the above functions. Again, the square brackets indicate the creation of a new list, the first expression in the square brackets describes what elements to add to the list, and the for clause indicates what sequence to traverse.

You can also use comprehensions to create tuples, dictionaries, and sets:

>>> tuple(i**2 for i in range(5))  # note including tuple is important
(0, 1, 4, 9, 16)
>>> {i**2 for i in range(5)}
{0, 1, 4, 9, 16}
>>> {i: i**2 for i in range(5)}
{0: 0, 1: 1, 2: 4, 3: 9, 4: 16}

Note how the syntax for set and tuple comprehensions is the same as list comprehensions, with the exception of what kind of brackets we use to surround the expression. For dictionary comprehensions, we need to include a key: value pair instead of a single element.

We can even make nested list comprehensions:

x = []
for outer in range(2):
    for inner in range(3):
        x.append((inner, outer))

print(x)  # [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1)]
y = [(inner, outer) for outer in range(2) for inner in range(3)]
print(y)  # [(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1)]

# this may seem confusing that the loops are reversed, but think of it
# as keeping the same loop structure, and moving the element we're appending
# to the front:

y = [(inner, outer)
        for outer in range(2)
            for inner in range(3)]

We can even use nested list comprehensions to create nested structures:

x = []
for i in range(3):
    row = []
    for letter in "abcd":
        row.append(letter + str(i))
    x.append(row)
print(x) # [['a0', 'b0', 'c0', 'd0'], ['a1', 'b1', 'c1', 'd1'], ['a2', 'b2', 'c2', 'd2']]

# can also be written as
y = [[letter + str(i) for letter in "abcd"] for i in range(3)]
print(y)

# think of simplifying row into a list comprehension first:
x = []
for i in range(3):
    row = [letter + str(i) for letter in "abcd"]
    x.append(row)

# we can think of row as the value we want to create for each element in
# our list x [row for i in range(3)]
# now substitute the actual list comprehension for row and you get
# the one line version in y

I'd recommend being careful with nested list comprehensions, because like ternary statements they tend to be more difficult to debug and can make code harder to read. However, they're a tool commonly used by experienced Python programmers, so you're likely to see code written like this in the 'wild'. It's also good to think of different ways to write the same code, so we'll get some practice with writing code more concisely in this week's exercises. Additionally, this should be helpful for completing some of your 15.066 assignments that use Python.

9) Variable Unpacking

It is often useful to swap the values of two variables. With conventional assignments, you have to use a temporary variable. For example, to swap a and b:

temp = a
a = b
b = temp

This solution is cumbersome; tuple assignment is more elegant:

a, b = b, a

The left side is a tuple of variables; the right side is a tuple of expressions. Each value is assigned to its respective variable. All the expressions on the right side are evaluated before any of the assignments.

The number of variables on the left and the number of values on the right have to be the same:

a, b = 1, 2, 3  # this produces: ValueError: too many values to unpack

This error message might seem weird, but this idea of assigning each element in a sequence to a different variable name is often referred to as unpacking that sequence.

For example, consider the following three pieces of code to compute the distance between points (where points are represented as (x, y) tuples.)

def distance(pt1, pt2):
    return ((pt1[0] - pt2[0])**2 + (pt1[1] - pt2[1])**2)**0.5

def distance(pt1, pt2):
    x1 = pt1[0]
    y1 = pt1[1]
    x2 = pt2[0]
    y2 = pt2[1]
    return ((x1 - x2)**2 + (y1 - y2)**2)**0.5

def distance(pt1, pt2):
    x1, y1 = pt1
    x2, y2 = pt2
    return ((x1 - x2)**2 + (y1 - y2)**2)**0.5

The first function definition is nice and to-the-point, but it is a bit hard to read because the indexing operations are all collapsed together with the mathematical operation to compute the distance. The second makes the last line easier to read, but at the expense of having to write 4 extra lines of code. The last, I think, strikes a nice balance between the two.

More generally, the right side can be any kind of sequence (string, list or tuple). For example, to split an email address into its username and domain name, we could do:

address = 'a_clever_username@mit.edu'
uname, domain = address.split('@')

The return value from split is a list with two elements; the first element is assigned to uname, the second to domain.

print(uname)  # prints a_clever_username
print(domain)  # prints mit.edu

Unpacking is also commonly used in for-loops, like iterating over dictionary key-value pairs:

en_de = {'dog': 'Hund', 'cat': 'Katze', 'guinea pig': 'Meerschweinchen'}

for key, value in en_de.items():
    print(key)
    print(value)

# equivalent to
for key in en_de:
    print(key)
    print(en_de[value])

10) Common Iterable Operations

An iterable object is anything we can loop over. In a typical for loop, we start by writing for element in SOME_VALUE: the SOME_VALUE part of this expression is an iterable. All of our sequences (list, tuple, string, range), dictionaries, and sets are iterables. Besides len, Python provides other nifty functions that we can use with iterables:

• max The max function can be called to find the maximum of two or more variables or iterates through an entire sequence to find the maximum value (note that each element in the iterable must be comparable).

>>> nums = [1, 2, 3, 4, 5]
>>> max([5, 4], nums)  # find max of two different values
[5, 4]
>>> max(nums)   # find max within an iterable
5
>>> max(set(nums))
5
>>> max( {"c": 5, "a": 1, "b": 3,})  # finds max dictionary key
'c'

However, we will run into errors if we try to find the max of an empty iterable or if it contains incomparable types:

>>> max(("a", 3, None))  # this tuple contains incomparable elements
    ...
TypeError: '>' not supported between instances of 'int' and 'str'
>>> max([])  # finding the max of an empty iterable will raise an error
    ...
ValueError: max() arg is an empty sequence
>>> max([], default=0)  # we can avoid this error by providing a default value
0

By design, sum and min functions act very similarly to max. sum totals all the elements together and returns a number, and min finds the minimum value.

>>> nums = [1, 2, 3, 4, 5]
>>> min(nums) # min acts like the opposite of max
1
>>> min([], default="")
''
>>> sum(nums) # sum assumes we are totaling numbers
15
>>> sum({"c": 5, "a": 1, "b": 3,})  # it won't add string dictionary keys
    ...
TypeError: unsupported operand type(s) for +: 'int' and 'str'
>>> sum([])  # because of this, it can sum an empty iterable without raising an error
0

sorted creates and returns a list containing the values sorted from smallest to largest.

>>> nums = [10, 5, 3, 1, 2]
>>> sorted(nums)
[1, 2, 3, 5, 10]
>>> sorted({3,5,1})
[1, 3, 5]
>>> sorted({"c": 5, "a": 1, "b": 2})
['a', 'b', 'c']
>>> sorted(nums, reverse=True) # sorts from largest to smallest
[10, 5, 3, 2, 1]

You can read more about these functions and other Python built-ins by referring to the Python documentation.

These functions are useful and can often help us avoid having to write for loops:

def max_func(nested_nums):
    # finds the max in each inner list of numbers nums,
    # and then finds and returns the max overall
    return max(max(nums) for nums in nested_nums)

    # equivalent to
    best = float("-inf")
    for nums in nested_nums:
        for num in nums:
            if num > best:
                best = num
    return best

    # or
    best = float("-inf")
    for nums in nested_nums:
        if max(nums) > best:
            best = max(nums)
    return best


print(max_func([[1, 2], [5, 6], [3, 4]]))  # 6

11) Imports and Dot Notation

Finally, let's talk about how to import and use Python modules. Python provides a large library of other functions and constants which are not available by default, but which can be imported and used within your code. These objects are available in collections called modules.

One common use of imports is to gain access to functions and constants defined in a Python module called math. Before we can use the objects in a module, we need to import them with an import statement, for example:

import math

This statement makes a module object in memory and associates it with the name math. In our environment diagrams, we'll denote this as:

We can access functions or constants from within the module using dot notation. For example, to look up and print the constant associated with the number e, we could do the following (after having used import as above):

print(math.e)

To evaluate an expression like this, Python first looks up the name math, finding the module stored in memory. The "dot" (.) then tells Python to look inside that module for something with the name e. In this case, because the math module does indeed contain something called e, it finds that object; so we would see:

2.718281828459045

The math module contains other constants (tau, pi, and others), and it also contains functions, such as sin and log³. We can look up these objects using dot notation as well, and then use them like so:

print(math.sin(3 * math.pi / 4))

import math
print(math.log(82, 3))

Importantly, module objects in many ways can be treated just like any other Python objects: For example, even though it is not a sensible thing to do, we could give another name to the math module after importing it:

import math
foo = math

This would result in the following environment diagram:

and then we could, for example, look up foo.sin and get the same sin function we would get from evaluating math.sin!

There is a lot of power in the math module, and it turns out that Python has a number of useful built-in modules that we can import from, as well (modules for dealing with strings, with e-mail, with generating random numbers, etc.). There are many more that we'll see later.

11.1) NumPy

NumPy is a widely-used library that provides fast operations for mathematical and numerical routines. NumPy, pronounced num-PIE, is an acronym for Numerical Python. NumPy is extraordinarily efficient because it is highly optimized for vector/matrix operations "under the hood" in ways that regular Python objects are not. In fact, for matrix solves, NumPy can be many thousands of times faster!

For right now, we're going to use numpy to help us with a simpler task: finding the mean, median, and standard deviation of a collection of numbers.

import numpy as np  # rename np as numpy so we don't have to type numpy.

# pick 50 random numbers between 1-100
rand_nums = [np.random.randint(1, 100) for i in range(50)]
print(np.mean(rand_nums))  # find average using numpy
print(sum(rand_nums) / len(rand_nums))  # find average using sum / len
print(np.median(rand_nums))
print(np.std(rand_nums))

Try running this program a few times. Each time you should notice it produces slightly different results, but because we have a medium-sized uniform random sample, statistically the mean and median should be around 50 and the standard deviation should be around 28.

You can read more about these functions and other NumPy methods by looking at the NumPy documentation.

11.2) Modules Beyond the Standard Library

While Python's standard library contains numerous useful modules, there are also modules available outside of the standard library; that is, modules which aren't installed by default with your Python installation. You can import these modules as well, and use them in the same way as above, after installing them on your machine. Usually installing them is a matter of running pip install package_name in a Terminal or Command Prompt, as you did at our kickoff to install numpy, scipy, and matplotlib.

12) Summary

In this reading, we introduced dictionaries and sets and saw a few sample programs involving them. We also learned how to import python modules, giving us access to the powerful python standard library.

In this set of exercises, you'll get some practice with dictionaries and sets. In the next set of readings and exercises, we will dive even further into functions and other modules.

Back to exercises