Readings for Unit 1

Licensing Information

The readings for 6.S090 are licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. You are free to make and share verbatim copies (or modified versions) under the terms of that license.

Portions of these readings were modified or copied verbatim from the very nice book Think Python 2e by Allen Downey.

PDF of these readings also available to download: reading1.pdf

Table of Contents

1) How To Use These Readings Effectively

When learning to program, it is not enough just to listen or to read; you need to practice! In this course, readings will introduce new ideas, but they will also ask you to participate!

There will be times on this page when you are asked to try things on your own. Some of these may be "checked" for correctness, but some are just suggested activities. Either way, it is important to do (and understand) all of these activities!

You will also occasionally be asked to type a program into Python. In these cases, we are really recommending that you type the program into Python verbatim, rather than using, e.g., copy and paste. It might seem like a small thing (and maybe tedious!), but it is important nonetheless! You'll find quite quickly that Python is very finnicky about the input it accepts; the act of typing the program out character by character, noticing mistakes if they exist, and comparing the code against what is shown on this page is good preparation for the detail-oriented work that is programming!

We are always here to help, but Morpheus said it perhaps best:

"I can only show you the door. You're the one that has to walk through it."
-Laurence Fishburne as Morpheus, The Matrix

We will try to provide you with all the materials and support you need, but it is up to you to make use of them (and also to let us know how best we can help you!).

2) Installing Python

You will need Python 3.6 or above installed to work through these readings and the associated exercises. If you do not already have access to Python, please see our instructions for accessing Python to get set up, and feel free to ask for help if you have trouble.

3) IDLE, and Your First Program

Regardless of your operating system of choice, Python should have come with an "integrated development environment" called IDLE¹. If you already have a text editor you prefer and you'd like to use that, you are welcome to; but our recommendation is to use IDLE if you don't have any other preference, as it is (relatively) simple and is made to work with Python.

Now that you have IDLE open, let's use it to write our first program. Under the "File" menu, choose "New File" (or simply hit Ctrl+N). A new window will open, with a blank text editor. Now it's time to write our first program and witness all of the raw power of programming first-hand. Type the following, exactly, into the new window:

print(2 + 3)

This program consists of a single print statement, which tells Python to display a value to the screen.

The rest might speak for itself: when we run it, this program will add the numbers 2 and 3 together and display the result to the screen.

To run the program, you'll first have to save it (find "Save" under the "File" menu, or hit Ctrl+S). Do this, and give it a name (for now, any name will do, though Python filenames typically end with .py). Once you have saved the file, find "Run Module" under the "Run" menu, or hit F5. When you do this, you will be taken back to the main IDLE window, and you'll see the result of running your program.

print 2 + 3

Missing parentheses in call to 'print'

NameError: name 'print2' is not defined

3.1) What is a Program?

A program (sometimes referred to as a script) is a sequence of instructions that specifies how to perform a computation. The computation might be something mathematical, such as solving a system of equations or finding the roots of a polynomial, but it can also be a symbolic computation, such as searching and replacing text in a document, or something graphical, like processing an image or playing a video.

The details look different in different languages, but a few basic instructions appear in just about every language:

• input: Get data from the keyboard, a file, the network, or some other device.
• output: Display data on the screen, save it in a file, send it over the network, etc.
• math: Perform basic mathematical operations like addition and multiplication.
• conditional execution: Check for certain conditions and run the appropriate code.
• repetition: Perform some action repeatedly, usually with some variation.

Believe it or not, that's pretty much all there is to it. Every program you've ever used, no matter how complicated, is made up of instructions that look pretty much like these. So you can think of programming as the process of breaking a large, complex task into smaller and smaller subtasks until the subtasks are simple enough to be performed with one of these basic instructions.

4) Our Goals

The ultimate goal of this course is to teach you to think in particular way, as an experienced programmer does. This way of thinking combines some of the best features of mathematics, engineering, and natural science. Like mathematicians, programmers use formal languages to denote ideas (specifically computations). Like engineers, they design things, assembling components into systems and evaluating tradeoffs among alternatives. Like scientists, they observe the behavior of complex systems, form hypotheses, and test predictions.

The single most important skill for a programmer is problem solving. Problem solving means the ability to formulate problems, think creatively about solutions, and express a solution clearly and accurately. As it turns out, the process of learning to program is an excellent opportunity to practice problem-solving skills. On one level, you will be learning to program, a useful skill in itself. On another level, you will use programming as a means to an end. As we go along, that end will become clearer.

We will spend a lot of time throughout the course trying to develop an appropriate mental model of Python, so that we can read, write, and debug our programs more effectively. We will develop a toolkit and a way of thinking that will empower you to create your own programs from basic building blocks, and to understand Python programs (both your own, and those written by others). Let's start right now by defining a few terms.

5) Primitive Objects, Values, and Types

For lack of a better way to say it, objects are the main things that Python programs work with. You've already worked with a couple of Python objects in the program you wrote above (specifically, 2 and 3)².

Each object has both a type and a value: an object's value determines the exact thing it represents, and its type determines the kinds of things that programs can do to it.

We will often refer to types as either primitive or compound. Primitive types are atomic: they are indivisible, and in some sense, they are the smallest pieces of the language that we can think about. Compound objects, as you might guess, are comprised of one or more primitive types.

Depending on how you count³, Python has around four primitive types, most of which represent different kinds of numbers:

1. int is a type used to represent integers. You've already experienced two integers in your first program: 2 and 3. Integers in Python are written the way we normally write integers, with one exception: commas cannot be used. So, for example, the following are integers: 2, 3, 0, -12, 10000.

2. float is a type used to represent real numbers. The most common way to specify a float is as a number with a decimal point. Any number with a decimal point in it is a float (for example, 5.0 or 6.2831 or 3.). There are a couple of other ways to specify floats, but we'll save those for another chapter.

   You might wonder why this type is not called "real" or "exact" or "decimal" ("float" seems like a pretty bizarre name, indeed!). The reason is that these values are represented in a computer in a representation called floating point. We won't go into detail about this representation in this class, but it is worth noting a few things:

   • This representation is used by almost all modern programming languages because it has some nice features.
   • However, it is worth noting that this representation cannot exactly represent all real numbers. As such, we will sometimes need to keep in mind that float objects are approximations of the numbers we actually want. To see an example of this behavior, modify your original program so that, instead of printing 2 + 3, it prints 0.1 + 0.1 + 0.1. Save and run your program, and you'll see an unexpected result!

3. bool is used to represent the Boolean values. In Python, these are represented as True and False.

4. NoneType is a type with a single value: None. None is a special kind of object that is designed to represent the absence of a value. This might seem weird for now (indeed, the number 0 felt weird to many civilizations for many centuries!), but it should come to make more sense with time.

5.1) Converting Between Numeric Types

It is sometimes possible to convert objects to a different type. For example, try int(7.8) or float(6). Converting a float to an int maybe doesn't do what we'd expect (it "truncates," i.e., it cuts off the decimal part altogether). Python also provides a way to round numbers using traditional rounding, for example round(7.8).

6) Algebraic Expressions

As we saw earlier, we are not limited to working with these basic types alone: we can combine them using operators. You've already experienced your first operator: +. Let's try some other operations.

print(2 + 3)
print(7 - 3)

You've also noticed that Python can do more than just add; it can subtract, as well! In fact, there are a few more operations we should introduce right now:

• + denotes addition.
• - denotes subtraction.
• * denotes multiplication.
• / denotes division.
• i**j denotes exponentiation (be careful about this! some other computer systems use a caret (^) to denote exponentiation, but in Python, the caret means something very different!)

7) A Model of Expression Evaluation

It's also worth noting that Python is not limited to expressions with a single operator. It can also handle more complicated expressions, like, for example:

2*3**2+4

How does Python handle such an expression?

7.1) Order of Operations

When an expression contains more than one operator, the order of evaluation depends on the order of operations. For mathematical operators, Python follows mathematical convention. The acronym "PEMDAS" is a useful way to remember the rules:

• Parentheses have the highest precedence and can be used to force an expression to evaluate in the order you want. Since expressions in parentheses are evaluated first, 2 * (3-1) is 4, and (1+1)**(5-2) is 8. You can also use parentheses to make an expression easier to read, as in (2 * 100) / 60, even if it doesn't change the result.

• Exponentiation has the next highest precedence, so 1 + 2**3 is 9 (not 27), and 3**2 * 2 is 18 (not 36).

• Multiplication and Division have higher precedence than Addition and Subtraction. So, 2*3-1 is 5 (not 4), and 6+4/2 is 8.0 (not 5.0).

Operators with the same precedence are evaluated from left to right. So, in the expression 7 / 2 * 3, the division happens first and the result is multiplied by 3. To divide by 2 * 3, you can use parentheses or write 7 / 2 / 3.

It's not necessary to work very hard to remember the precedence of operators. If you can't tell by looking at the expression, you can use parentheses to make the order in which things are happening more obvious.

7.2) The Substitution Model

Our first model of expression evaluation is the substitution model: when Python evaluates an expression, it works down the order of operations, evaluating subexpressions and replacing each with its result. For example, consider evaluating the expression 2*3**2+4.0

Python will honor the order of operations, first evaluating 3**2 to find 9, and substituting that value into the original expression. After this step, we now have: 2*9+4.0.

Again, following the order of operations, Python will next evaluate 2*9 to find 18, and substitute that value into the expression. After this step, we have: 18+4.0.

Finally, Python evaluates 18+4.0 to find 22.0, which is the result of evaluating the entire expression.

8) Boolean Expressions

A Boolean expression is an expression that is either true or false, and evaluates to an object of type bool whose value is either True or False.

The following examples use the operator ==, which compares two operands and produces True if they are equal and False otherwise:

print(5 == 5)
print(5 == 6)

This example will print True on one line, and False on the next.

The == operator is one of the relational operators (which operate on arbitrary values and produce bool objects); the others are:

• == ("is equal to") compares two operands and produces True if they are equal, and False otherwise.
• != ("is not equal to") compares two operands and produces True if they are not equal, and False otherwise.
• > ("is greater than") compares two operands and produces True if the first is greater than the second, and False otherwise.
• < ("is less than") compares two operands and produces True if the first is less than the second, and False otherwise.
• >= ("is greater than or equal to") compares two operands and produces True if the first is greater than or equal to the second, and False otherwise.
• <= ("is less than or equal to") compares two operands and produces True if the first is less than or equal to the second, and False otherwise.

Although these operations are probably familiar to you, the Python symbols are different from the mathematical symbols. A common error is to use a single equal sign (=) instead of a double equal sign (==). But it turns out that = has a different meaning in Python, which we'll discuss in the following section.

There are also three operators that operate exclusively⁴ on Boolean values:

• and produces True if both of its operands are True, and produces False otherwise (for example, True and True produces True; but False and True produces False).
• or produces True if at least one of its operands is True, and produces False otherwise (for example, True or True produces True; and True or False also produces True; but False or False produces False).
• not is a unary operator (it has only one operand) that produces True if its operand is False, and False if its operand is True (for example, not False produces True; and not True produces False.

8.1) Adding to Order of Operations

Python expressions can grow complicated and can contain any number of the operators listed above (including both arithmetic and Boolean operators).

We need to know how these new operators work in our substitution model for expression evaluation. In particular, the order of evaluation is as follows:

• Arithmetic operations happen first, in the order described above.
• Then the <, >, <=, and >= comparators are evaluated. These all have the same precedence, so they are evaluated from left to right.
• Then the == and != operators are evaluated from left to right.
• Then the not operator is evaluated.
• Then and
• Then, finally, or.

9) Variables and Assignment

One of the most powerful features of a programming language is the ability to manipulate variables. Simply put, a variable is a name that refers to a value.

We create a new variable and associate it with a value with an assignment statement, which makes use of the assignment operator (the "equals" sign, =). For example, the following short piece of code associates the name x with the value 4.

x = 2+2

It's important to note that this operator does not work like the "equals" sign in regular algebra. Rather, Python will respond to this kind of statement by evaluating the expression on the right side of the assignment operator, and then associating the name on the left side of the operator with the resulting value.

This statement is not really saying "x is equal to 2+2", at least in the sense that you might be familiar with from mathematics. Rather, what it really tells Python: compute the value 2+2, and associate the name x with the result.

Once Python has this association, we can include x in an expression, just like we could any other value in Python. For example, we could say:

print(x + 7)

when Python evaluates this print statement, it must compute x + 7. Conveniently, it will remember the value that was associated with x, and the above will print 11.

9.1) Valid Variable Names

Python only allows certain names for its variables. Python variable names must contain only letters, numbers, and the underscore character; furthermore, they must start with either a letter or an underscore. Variable names with other characters in them are not allowed.

Python also has several keywords, which are not allowed as variables because they have other meaning in the language. These are: False, None, True, and, as, assert, async, await, break, class, continue, def, del, elif, else, except, finally, for, from, global, if, import, in, is, lambda, nonlocal, not, or, pass, raise, return, try, while, with, yield.

9.2) Choosing Variable Names

There is a lot of freedom in choosing variable names in the programs you write, but it is a good idea to try to balance choosing descriptive variable names with choosing short variable names that are reasonably easy to type.

For example, it is very difficult to tell what the following program does because of poorly chosen variable names:

a = 6.28318
b = 2

c = a * b
d = 1 / 2 * a * b ** 2

e = 4 * d
f = 2 / 3 * a * b ** 3

Its readability could be drastically improved by choosing variable names more carefully:

tau = 6.28318
radius = 2

circle_circumference = tau * radius
circle_area = 1 / 2 * tau * radius ** 2

sphere_surface_area = 4 * circle_area
sphere_volume = 2 / 3 * tau * radius ** 3

Of course, it is possible to go too far in the direction of descriptive variable names. The following code, which borders on the absurd, is maybe even more of a pain to read than the first example:

the_ratio_between_the_circumference_and_the_radius_of_a_circle = 6.28318
the_radius_of_the_shapes_for_which_we_want_to_compute_values = 2

the_circumference_of_a_circle_with_the_radius_given_by_the_variable_defined_above = the_ratio_between_the_circumference_and_the_radius_of_a_circle * the_radius_of_the_shapes_for_which_we_want_to_compute_values
the_area_of_a_circle_with_the_radius_given_by_the_variable_defined_above = 1 / 2 * the_ratio_between_the_circumference_and_the_radius_of_a_circle * the_radius_of_the_shapes_for_which_we_want_to_compute_values ** 2

the_surface_area_of_a_sphere_with_the_radius_given_by_the_variable_defined_above = 4 * the_area_of_a_circle_with_the_radius_given_by_the_variable_defined_above
the_volume_of_a_sphere_with_the_radius_given_by_the_variable_defined_above = 2 / 3 * the_ratio_between_the_circumference_and_the_radius_of_a_circle * the_radius_of_the_shapes_for_which_we_want_to_compute_values ** 3

Interestingly, Python will happily run any of these files, and the results will be the same! But it's important to write programs not only with an eye toward correctness, but also with an eye toward clarity.

10) Environment Diagrams

Earlier, we started building up our mental model of how Python behaves by developing the substitution model for expression evaluation. Now, with variables in the mix, we'll have to expand our model.

In this section, we'll talk through how Python would evaluate a short program, using a particular type of drawing (called an environment diagram) to help keep track of things.

In addition to being able to evaluate expressions, Python also has some memory. For now, we'll think of memory as an abstract place where Python keeps track of objects. In our drawings, we'll typically denote Python's memory with an amorphous blob:

When Python needs to remember an object, that object is stored in memory. In addition, Python needs a way to associate names with the objects it has stored. It does this via a construct called a frame, which we can think of as a lookup table: given a name, it points us to the associated object in memory.

For now, our model is going to consist of exactly one frame, which we refer to as the Global Frame. Given the tools we currently have available, this is where the mappings from name to object will be kept⁵.

Our starting point for an environment diagram will contain both this abstract idea of memory, and the Global Frame. For now, we will think of the Global Frame as being completely empty when Python starts. When Python first starts, our current model (in the form of an environment diagram) looks like this:

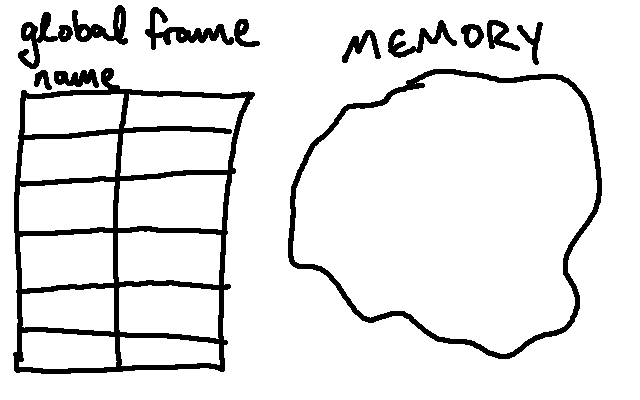
As new assignments are made, Python will store the relevant objects in memory and make new associations in the Global Frame. As an example, let's consider the following program:

x = 300
print(x + 2)
y = 2 + 5
z = x + y
y = x
print(z)

Remember that Python will evaluate this program one line at a time. It starts by evaluating the first line, x = 300. When Python evaluates this line, it stores the result of the expression to the right of = in memory (in this case, 300), and it associates the name x with that value. In our environment diagrams, we can denote this relationship by putting a 300 in memory, making an entry in the Global Frame for x, and drawing an arrow from x to the new value.

After executing that line, our environment diagram now looks like this (here we've drawn the arrow in blue just so that it stands out a bit):

Then we run the following line, print(x + 2). When running this line, Python must evaluate x + 2. In order to account for this, we need our substitution model to be able to account for variables. Simply put, when Python gets to a point where it needs to evaluate a variable, it will look it up in the global frame and substitute in the associated value.

In this case, we have:

• x + 2 (look up value of x, which gives...)
• 300 + 2 (compute addition, which gives...)
• 302

so 302 will be displayed to the screen.

Next, Python will execute the line: y = 2 + 5. Once again, Python will evaluate the expression to the right of the equals sign (2 + 5), store the result in memory as 7, and associate the name y with that object:

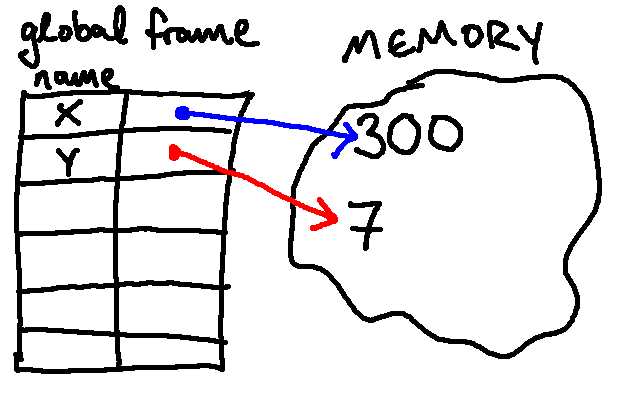
Then Python will execute: z = x + y. Once again, it evaluates the expression on the right side of the = sign. Using our substitution model, this is evaluated as:

• x + y
• 300 + y
• 300 + 7
• 307

The value 307 is stored in memory, and the name z is associated with the value 307:

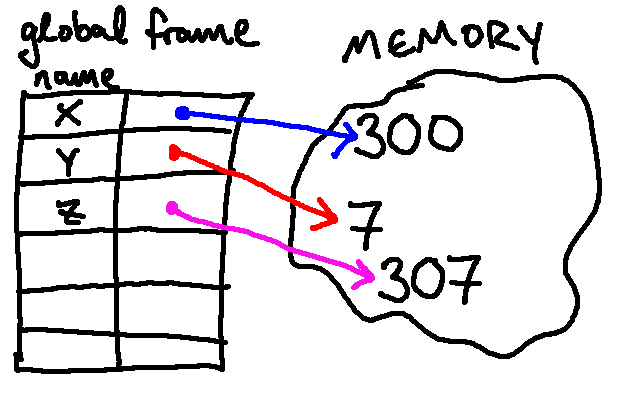
Next, we evaluate y = x. This changes the value associated with y, so that y is now associated with the result of evaluating x (300). Graphically, this results in the following:

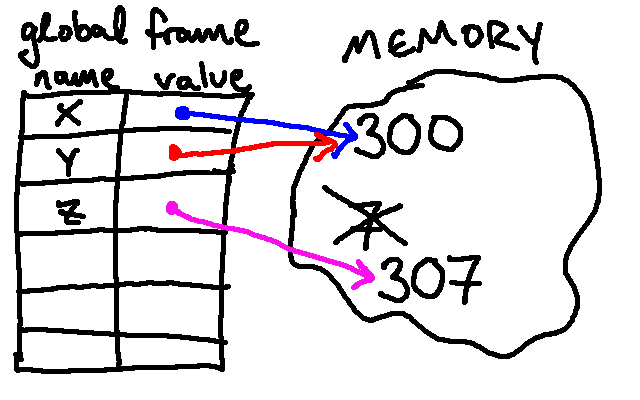
Note two things about this updated diagram:

1. The value y now points to the exact same object that is associated with the name x (because we found that object by looking up x and following its arrow to an object in memory). If we had instead said y = 300, we would instead make a new object with the same type and value as our original 300 and y would point to that (and so, in that case, we would have had two different 300 objects in memory, with x pointing to one of them and y pointing to the other⁶).

2. After the definition of y is updated, there are no names associated with the 7 in memory anymore. Typically, when there is a value in memory with no variables referencing it, Python will remove it from memory. This process is called garbage collection because it involves cleaning up the left-over objects in memory that are no longer being used. In our environment diagrams, we'll cross out objects that have been "garbage collected."

Finally, when executing print(z), Python looks up z, which is still associated with the value 307 (despite the fact that y's association changed), so 307 is printed.

Try Now:

Consider the following short Python program:

x = 4
x = x + 1
print(x)

Draw an environment diagram that represents the evolution of this program, and use it to predict what value will be displayed on the screen when this program is run. Once you have drawn your diagram and made your prediction, run this program. Does the result match what you predicted?

Show/Hide

Initially x is associated with the value 4. On the second line, however, we evaluate x + 1 (getting 5 as a result), and we modify x's association so that it now points to that new value. Because the 4 object is left with no references pointing to it, it is "garbage collected." So we end up with the following diagram:

That second line might be frightening if you have in mind the meaning of the "equals sign" from algebra. But this should not scare us here! To Python, it says: compute the result of x+1, and associate the name x with the result.

11) Conditional Execution

So far, all of our programs have continued in a relatively straightforward manner: Python executed all of the statements in a program in exactly the order they were specified:

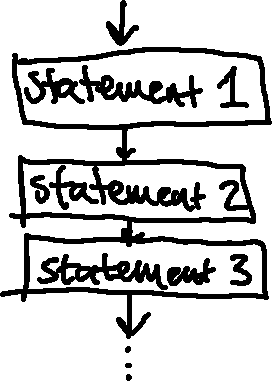
In order to write useful programs, however, we almost always need the ability to check conditions and change the behavior of the program accordingly. Conditional statements give us this ability. The simplest form is the if statement, like this one to set x to its absolute value:

if x < 0:
    x = -x

The boolean expression after if is called the condition. If it is true (i.e., if it evaluates to True), the indented statement (the body) runs. If not, nothing happens. This structure is represented by the following flow chart:

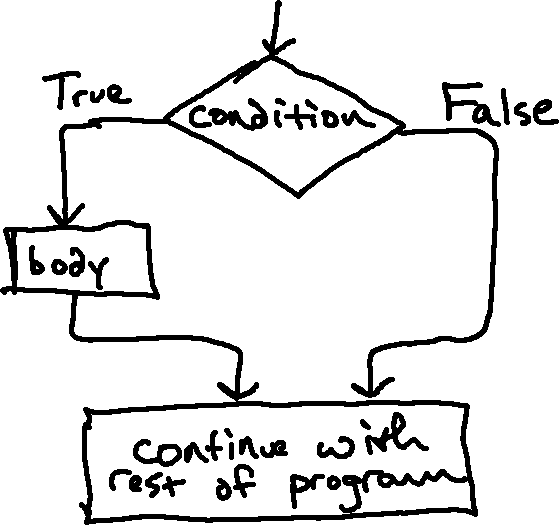
Note that we could have multiple statements in the body as well; any statements that are indented at the same level are all part of the body, and they are all executed if the condition is true. For example:

print("This will always print")
if x < 0:
    print("x is negative")
    print("so we'll print")
    print("a few extra things")
print("This will always print, too")
print("And so will this!")

(Note that this example also introduces a new concept: we can display a sequence of characters to the screen verbatim by surrounding them in quotes.)

In this case, if x is less than 0, Python will execute all three indented lines; otherwise, it will skip all of them. Notice that only the execution of those indented lines is affected by the condition; the bottom two lines are not part of the conditional; they are always executed.

There is no limit on the number of statements that can appear in the body, but there has to be at least one. Occasionally, it is useful to have a body with no statements (usually as a placeholder for code you haven't written yet). In that case, you can use the pass statement, which does nothing.

if x < 0:
    pass

if statements have an interesting structure: a header followed by an indented body. Statements like this are called compound statements. We will learn about a few more kinds of compound statements throughout the rest of the course.

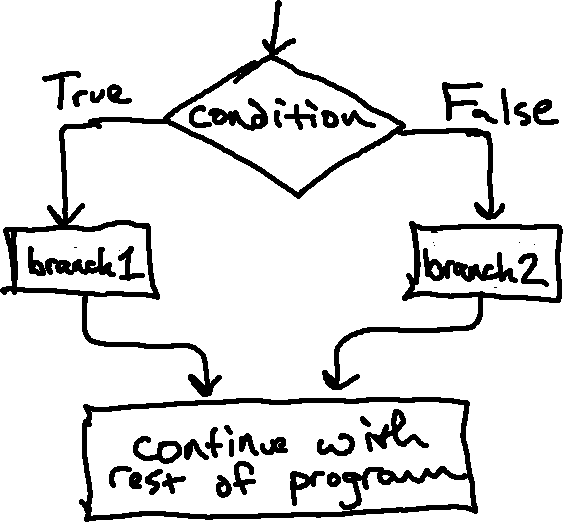
A second form of the if statement is "alternative execution," in which there are two possibilities and the condition determines which one runs. The syntax looks like this:

if x % 2 == 0:
    print("x is even")
else:
    print("x is odd")

If the remainder when x is divided by 2 is 0, then we know that x is even, and we print a message to that effect. If the condition is false, the second set of statements runs. Since the condition must be true or false, exactly one of the alternatives will run. The alternatives are called branches, because they are branches in the flow of execution.

This structure (alternative execution) is represented by the following flow chart:

11.1) Chained Conditionals

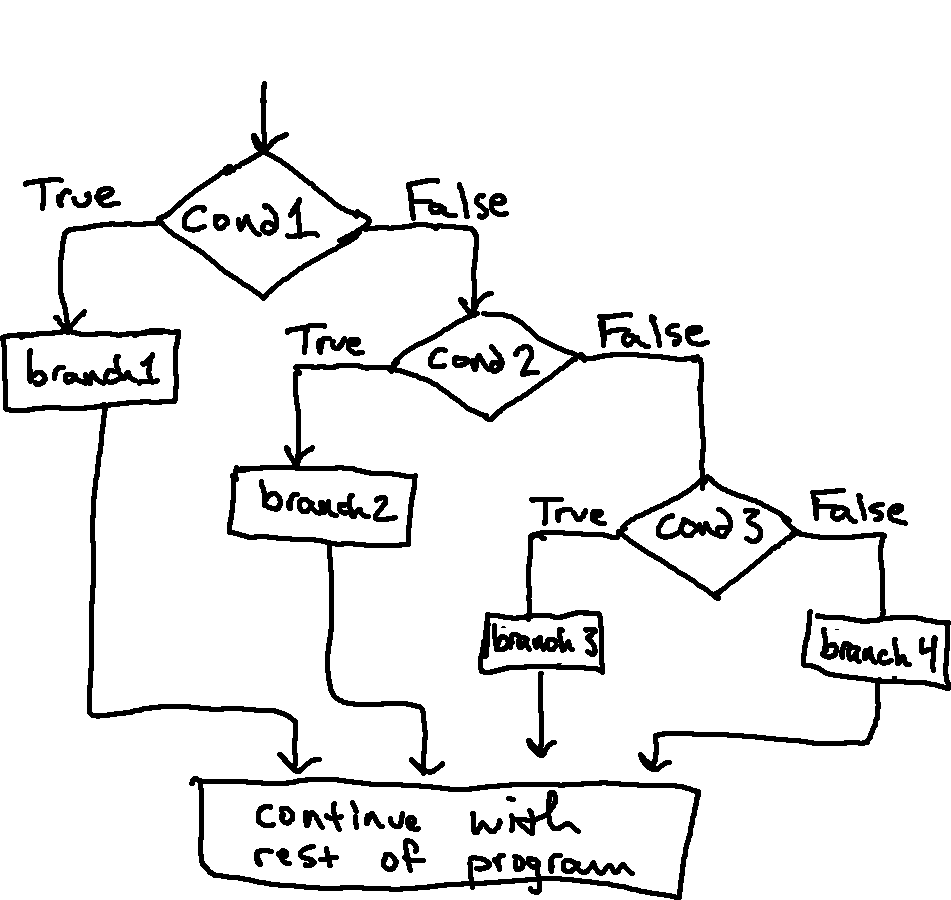
Sometimes there are more than two possibilities and we need more than two branches. One way to express a computation like that is a chained conditional:

if x < y:
    print('x is less than y')
elif x > y:
    print('x is greater than y')
else:
    print('x and y are equal')

elif is Python's abbreviation of "else if". Again, exactly one branch will run. There is no limit on the number of elif statements. If there is an else clause, it has to be at the end, but there doesn't have to be one.

if choice == 'a':
    print('The choice was a')
elif choice == 'b':
    print('The choice was b')
elif choice == 'c':
    print('The choice was c')
else:
    print('The choice was something else...')

Each condition is checked in order. If the first is false, the next is checked, and so on. If one of them is true, the corresponding branch runs and the statement ends. Importantly, even if more than one condition is true, only the first true branch runs.

The structure of the code just above is shown in the following flow chart:

if True:
    print('inside first branch')
elif True:
    print('inside second branch')
else:
    print('inside third branch')

11.2) Nested Conditionals

The branches of a conditional can contain arbitrary Python code. This means that, among other things, one conditional can also be nested within another. We could have written the example in the previous section like this:

if x == y:
    print("x and y are equal")
else:
    if x < y:
        print("x is less than y")
    else:
        print("x is greater than y")

The outer conditional contains two branches. The first branch contains a simple statement. The second branch contains another if statement, which has two branches of its own. Those two branches are both simple statements, although they could have been conditional statements as well.

Although the indentation of the statements makes the structure apparent, nested conditionals can often become difficult to read very quickly. It is a good idea to avoid them when you can.

Logical operators often provide a way to simplify nested conditional statements. For example, consider the following code:

if 0 < x:
    if x < 10:
        print("x is a positive single-digit number.")

The print statement runs only if we make it past both conditionals, so we can get the same effect, but nicer style, by using the and operator:

if 0 < x and x < 10:
    print("x is a positive single-digit number.")

12) Functions

def f(x):
    return x + 1

We can call (or use) the function f after it is defined as follows:

f(5)
num = 7.5
f(num)

print(f(5))
num = 7.5
print(f(num))

6
8.5

The indentation is important here, too. All of the statements of the function have to be indented one level below the def.

Here's another function example:

def rectangle_area(width, height):
    print("Calculating rectangle area...")
    if width < 0 or height < 0:
        print("Rectangle height / width cannot be negative!")
    else:
        return height * width

print("This is outside the function!")
print("Result of the first call", rectangle_area(5, 4))
print("Result of the second call", rectangle_area(10, -1))

This is outside the function!
Calculating rectangle area...
Result of the first call 20
Calculating rectangle area...
Rectangle height / width cannot be negative!
Result of the second call None

Functions are useful for many reasons, including that they allow programmers to re-use and separate parts of code. Note that functions are also sometimes referred to as procedures or methods. Stay tuned for more fun with functions in future readings!

13) Comments

"Commenting your code is like cleaning your bathroom - you never want to do it, but it really does create a more pleasant experience for you and your guests."
-Ryan Campbell

Our programs so far have been relatively small, but as programs get bigger and more complicated, they get more difficult to read. Programming languages are dense, and it is often difficult to look at a piece of code and figure out what it is doing, or why.

For this reason, it is a good idea to add notes to your programs to explain in natural language what the program is doing. These notes are called comments, and they start with the # symbol⁷:

# compute the percentage of the hour that has elapsed
percentage = (minute * 100) / 60

In this case, the comment appears on a line by itself. You can also put comments at the end of a line:

percentage = (minute * 100) / 60     # percentage of an hour

Everything from the # to the end of the line is ignored; it has no effect on the execution of the program.

Comments are most useful when they document non-obvious features of the code. It is reasonable to assume that the reader can figure out what the code does; it is more useful to explain why.

This comment is redundant with the code and useless:

v = 5     # assign 5 to v

By contrast, this comment contains useful information that is not in the code:

v = 5     # velocity in meters/second

Good variable names can reduce the need for comments, but long names can make complex expressions hard to read, so there is a tradeoff.

It is also possible to write longer multi-line comments in Python as shown below:

''' <- These three single quote marks begin the multi-line comment.

This is the body of the comment.
print("Python will ignore this print statement when it is part of a comment.")

These three single quotes end the multi-line comment. ->'''

print("Python will run this print statement.")

"""
Multi-line comments can also be created using three double quotes - all that matters is that the start quotes match the end quotes!
"""

Multi-line comments are often used to document the purpose of a function or a larger block of code.

14) Bugs

Unfortunately, like most other kinds of people, programmers occasionally make mistakes. This is true at all levels of experience, and even for programmers who are being very careful to avoid errors.

For interesting historical reasons, issues in computer programs are referred to as bugs⁸, and the act of fixing these errors is called debugging.

In this section, we'll talk briefly about a few kinds of bugs that might show up in your programs, and why. Throughout the course, we'll work toward understanding how to locate and eliminate these bugs.

14.1) Errors: Lost in Translation

It is up to us to translate our high-level plan for what we want our program to accomplish into a formal language that the computer (in particular, the Python interpreter) can understand. The rigidity of most programming languages presents a barrier, in part because they are so different from the languages we speak in everyday life.

In Englih, fi we msspell a wrod or tooo, yuo mite stil undrstnd wot we right. Or if we makes a grammatical mistakes, you can often still grasped my meaning. Natural languages (the languages that people speak, like English or Spanish, which evolve naturally) are robust against several kinds of errors or ambiguities, because they are interpreted by humans. When interpreting sentences in a natural language, we often use contextual clues, prior knowledge, and redundancy to deal with things like ambiguity and idiom.

Whereas natural languages are generally relatively free in form and are full of ambiguity and idiom, formal languages, by contrast, tend to be very rigid in structure and literal in meaning. Python is an example of a formal language designed to express computations. Unfortunately, the computer cannot rely on contextual clues or prior knowledge to help deal with inaccuracies or ambiguities in the programs we give to it, and so we have to translate our plans into Python very carefully.

Because most of our experience involves working with natural languages, it can be difficult for us to translate ideas into a formal language. We can already understand two types of errors that can result as a part of this translation process: syntax errors and runtime errors.

• Syntax Errors: "Syntax" refers to the structure of a program and the rules about that structure. For example, parentheses have to come in matching pairs, so (1 + 2) is syntactically valid, but 8) is not; it is a syntax error. Python is very particular about the syntactic structure of programs it evaluates.

  If there is a syntax error anywhere in your program, Python displays an error message and quits, and you will not be able to run the program. During the first few weeks of your programming career, you might spend a lot of time tracking down syntax errors. As you gain experience, you will make fewer errors and find them faster.

• Runtime Errors: The second type of error is a runtime error, so called because the error does not appear until after the program has started running. These errors are also called exceptions because they usually indicate that something exceptional (and bad) has happened.

  This kind of error results in many cases when a syntactically-valid program has other issues. For example, the expression x + y is always syntactically valid, but if x has value None and y has value 6 when that expression is computed, Python will quit with a TypeError, stating that the types of the two operands were incompatible with the operation in question.

  Another example would be trying to, for example, print(some_variable) if some_variable hadn't been defined yet. There's nothing syntactically wrong with that expression, and so Python won't notice it until it tries to run. Once again, Python will quit in a storm of red text (this time, with a NameError because it is unable to find the name in question in the Global Frame).

  Runtime errors are somewhat rarer in the simple programs you will see in the first few assignments.

14.2) Semantic Errors

"I really hate this damned machine
I wish that they would sell it.
It never does quite what I want
But only what I tell it."
-A Programmer's Lament

In some sense, there is something nice about the two kinds of errors in the previous section: Python complains very loudly for both kinds of errors. It stops executing any code and reports an error message.

But there is yet another kind of error that has not been discussed yet, and it is far more subtle. For example, what is the error in the following program, designed to compute the absolute value of x?

def absolute_value(x):
    if x > 0:
        return -x
    else:
        return x

This code is completely backward, and will never print a positive number! But as far as Python is concerned, there is no error; there is no way for Python to know that this was not the behavior we intended, and so it will happily chug along. This kind of error might be especially dangerous if this result is used elsewhere in the code (using the erroneous result might cause bigger issues elsewhere!).

This kind of error is known as a semantic error ("semantic" means: related to meaning). If there is a semantic error in your program, it will run without generating error messages, but it will not do the right thing. It will do something else. Specifically, it will do exactly what you told it to do.

Because these types of errors are so insidious, we will take great care throughout this course (particularly once we have developed more tools in the later sections) to test individual pieces of our programs to make sure they are working before joining them together.

15) Testing

Here are some example tests:

def absolute_value(x):
    if x > 0:
        return -x
    else:
        return x

if __name__ == "__main__":
    # Testing absolute_value function with different possible inputs:
    print(absolute_value(-5))  # this should print 5
    print(absolute_value(3.6)) # this should print 3.6
    print(absolute_value(0.0)) # this should print 0.0

-5
-3.6
0.0

Note that placing code used for debugging functions inside a if __name__ == "__main__": statement at the bottom of the .py file is good Python practice.

16) Summary

In this first reading, we covered a lot of ground. At this point, our mental model of Python includes several pieces:

• A notion of several types of Python objects (int, float, ...)
• Myriad operators for combining these objects (+, <, and, ...)
• A model for how Python evaluates expressions (the substitution model)
• A model for how Python stores objects in memory (environment diagrams)
• A means of controlling the flow of programs (conditional execution)
• A means of re-using code with different inputs (functions)

In this set of exercises, you'll get some practice with all of these tools. In the next set of readings and exercises, we will expand on these models. In particular, we will introduce several new types of Python objects and a few new tools for controlling the flow of programs.