Readings for Unit 2

Licensing Information

The readings for 6.S090 are licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. You are free to make and share verbatim copies (or modified versions) under the terms of that license.

Portions of these readings were modified or copied verbatim from the very nice book Think Python 2e by Allen Downey.

PDF of these readings also available to download: reading2.pdf

Table of Contents

1) Introduction

In the last set of readings, we introduced several types of Python objects, as well as models of how Python evaluates expressions and how it manages storing and looking up variables. We also introduced our first means of controlling the order of the evaluation of statements in a program through conditional execution and showed how we could re-use code by defining and calling functions.

In this reading, we will introduce and explore some new types of Python objects, and we'll see how to fit these new types into our existing framework. We'll also introduce some new control flow mechanisms.

Before you dive into this unit, you may wish to review some of the readings and exercises from last week. Almost everything introduced in this unit will build on ideas from the last one.

2) Strings

In the last set of readings, we saw that we could display characters to the screen verbatim by enclosing them in quotation marks in a print statement. For example, running the code below will display hello, python! on the screen:

print("hello, python!")

But at the time, we didn't talk much about what this statement actually meant in terms of our mental model of Python. In this section, we'll start to clarify this a bit by introducing a new Python type into our mental model: strings.

A string is a type that represents a sequence of characters¹. In Python, this type is given the name str. It turns out, also, that it is fine to use either double quotes (") or single quotes (') to enclose strings.² So the Python expression "yarn" evaluates to a string, and so does 'twine'.

Because strings are actually a type of Python object, it turns out that we can do more than just print them! We can, for example, store a string in a variable:

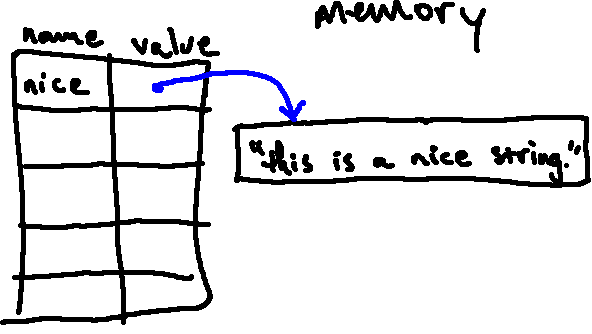
nice = "This is a nice string."

We can think of this the same way we thought of other variable assignments:

• Python will start by evaluating the value on the right side of the = symbol (which, in this case, results in a string).
• It will then store this string in memory, and associate the name nice with it.

Much like we did with int and float objects, we can denote strings in our environment diagrams by simply writing their value, though it may be a good idea also to draw a box around a string so that it's clear that it is a single object. Running the above code snippet, for example, would result in the following environment diagram:³

Once we have the string stored in a variable, we can include the variable in other expressions. For example, after making the definition above, we could print that string with:

print(nice)

This will look up the variable name nice in the global frame; doing so, it finds the string that is stored in memory, which it then displays.

favorite_animal = "dog"
favorite_language = "python"
print(favorite_animal)
print(favorite_language)

favorite_animal = "dog"
favorite_language = "python"
print("favorite_animal")
print("favorite_language")

2.1) Concatenation (e.g., 'hello ' + 'world')

We saw in the last set of readings that the type of an object is important for determining the kinds of operations we can perform on that object. For example, we could perform arithmetic with int and float objects, but not with NoneType objects. Similarly, we can perform some kinds of operations on strings. Specifically, we can concatenate (combine) two strings together using the + operator.

print("I'm adding this string" + "to this string")

Try Now:

Draw an environment diagram that shows the result of running the following short program, and predict what it will print:

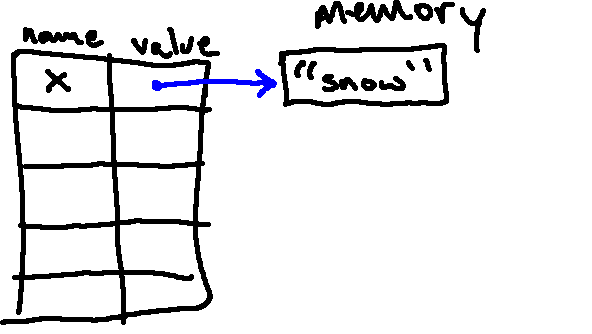
x = "snow"
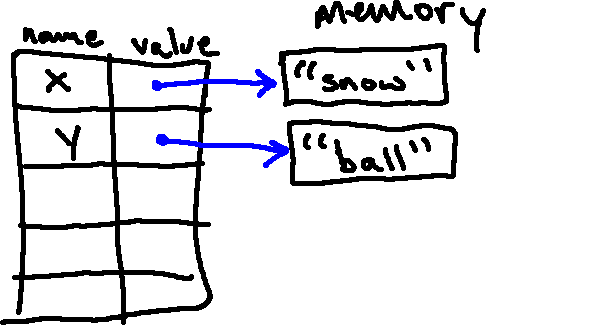
y = "ball"

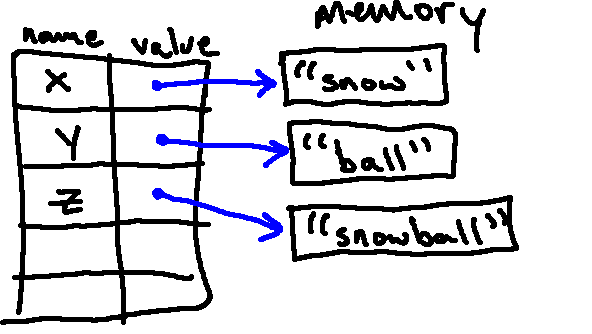
z = x + y

x = "basket" + y

print(z + " " + x)  # the middle string contains a single "space" character

Show/Hide

After executing the first line, we have the object "snow" in memory, and the name x associated with it:

After the following line, we have a second object, "ball", in memory, and the name y associated with it:

In the process of evaluating the third statement, Python looks up x (finding "snow") and y (finding "ball"), and concatenates them to form a new string, "snowball". This object is stored in memory, and the name z is associated with it:

Next, we replace the definition of x with the result of evaluating "basket" + y. This evaluation gives us the new string "basketball", which we then associate with x. After we do this, there are no references left to our original "snow" object, so it is garbage collected, giving us the following final diagram:

The final line contains a print statement, and we can use our substitution model to determine the value that is printed:

• z + " " + x (Loading z gives us...)
• "snowball" + " " + x (Concatenating the first two terms gives us...)
• "snowball " + x (Loading x gives us...)
• "snowball " + "basketball" (Concatenating these two strings gives us...)
• "snowball basketball"

And so the value that is printed is "snowball basketball".

2.2) Boolean Equality (==, !=)

In last week's reading, we saw how Python can use the boolean operators we've discussed (!=, ==, >=, <=, >, <) to compare numbers with each other (and combining / comparing int objects with float objects tends to work as we would expect). More generally, Python can check if any two objects are equal using == or check if they are not equal using !=, even if the objects do not have the same type. While in the last reading we saw that we can perform the other comparisons (<, >, >=, <=) between int objects and float objects, usually Python will only perform these comparisons when the two objects have the same type.

2.3) Length (e.g., len("hello"))

Another useful function that works on strings is the len function. It can take a single string as input and return the number of characters in the string as an int. For example, calling len("hello") would return 5.

sentence = " How many characters are in this sentence?"
print(len(sentence))

2.4) Indexing (e.g., "hello"[0])

You can ask Python for one character from a string with the bracket operator. For example, try the following:

fruit = "banana"
letter = fruit[1]
print(letter)

The second statement selects character number 1 from fruit, stores it in memory, and associates the name letter with it. The expression inside the brackets (in this case, 1) is called an index. The index, which must be an integer, indicates which character in the sequence you want.

But, running the code above, you might not get the answer you expect!

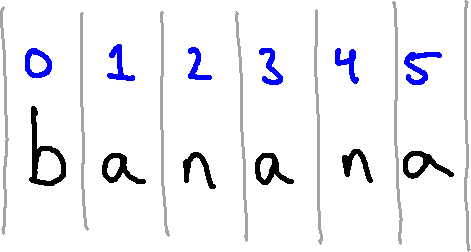
Most people would expect character one from "banana" to be "b". But in Python (as in many programming languages), we actually start counting at 0 rather than at 1⁴.

So the indices from 0 to 5 are associated with the letters in this string as shown below:

It is perhaps also worth noting that you can also index from the end of a string. The index -1 is associated with the last character in a string, -2 with the next to last, and so on. So we really have two indices associated with each character:

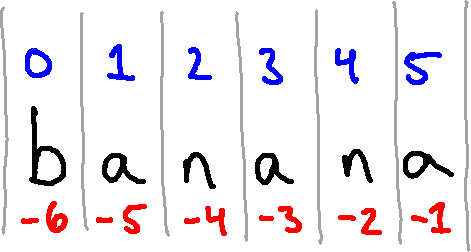
Trying to access an index other than one of those numbers (in this case, integers between -6 and 5, inclusive) results in an error.

3) Other Sequences

Strings are an example of a compound type: they are sequences of characters. But you may be wondering, is there a way to store sequences of other kinds of information (like numbers)? Yes! We will now introduce two additional types of Python sequences: tuples⁵ and lists.

3.1) Tuples (e.g., (7, -7.8, "blue"))

Tuples are sequences like strings, with the important distinction that, while strings are limited to containing only characters, tuples can contain arbitrary objects, such as integers, floats, Booleans, None, or even other tuples!

A tuple is specified as a comma-separated sequence of arbitrary objects, usually wrapped in parentheses. For example, the following is a tuple containing three different objects:

x = (7, -7.8, "blue")

We can perform many of the same operations on tuples that we could on strings. For example:

• we can use + to concatenate two tuples (x + (1, 2, 3) which gives us a new tuple (7, -7.8, "blue", 1, 2, 3))
• we can compare tuples for equality ((1, 2) != (2, 1) results in True because equality for sequences is defined as having the same elements in the same order)
• we can check the length of the tuple (len(x) results in 3 because the tuple x has three elements. len(x + (x,)) results in 4 because the tuple that results from the concatenation has the three elements from the first tuple followed by the single element in the second tuple.)
• we can index into a tuple (x[1] gives us -7.8)

We also need a way to represent tuples in our environment diagrams, to model how Python actually handles them in memory. We will model the above tuple (7, -7.8, "blue") with the following kind of drawing:

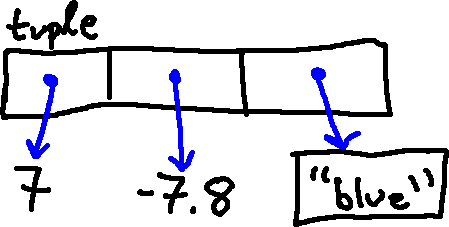
We'll draw it as a box, with the label "tuple" (so that we can keep track of types), with several references to other objects. You can think of these references as being very similar to the mappings we have already considered, from names to objects.

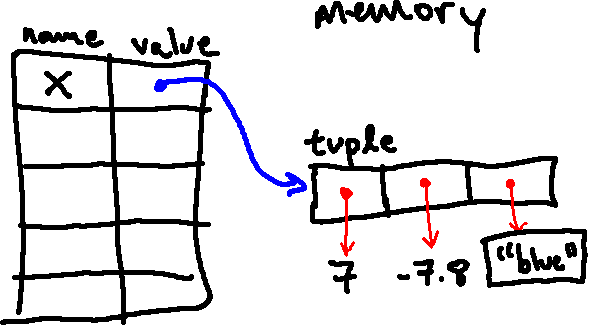
So after evaluating the line of code above (x = (7, -7.8, "blue")), we will have the following environment diagram:

Let's examine what happens when we index into x. Consider, for example, running the following code:

print(x[-1])

Python first looks up x in the global frame. Doing so, it follows the pointer from x and finds the tuple object in memory. Then, it looks up index -1 inside of x. This is the last "slot" in x, and so, following that pointer, we find the string "blue".

Notice here that x[-1] is still a string, and so anything we can do to any other string, we can do to x[-1]. This includes indexing into it! So we could try the following:

print(x[-1][2])

When evaluating x[-1][2], Python will first look up x (finding the tuple in memory). Then it will look up index -1 inside of that tuple (finding the string "blue"). Finally, it will look up index 2 of that string (finding "u"). So this line above with print a u to the screen.

Try Now:

Try drawing an environment diagram for the following code:

a = 1
b = 2
c = 3

x = (c, b, a)
y = (3, 2, 1)

What is different about how the two tuples are represented in memory?

Show/Hide

After executing the first three lines, our environment diagram looks like this:

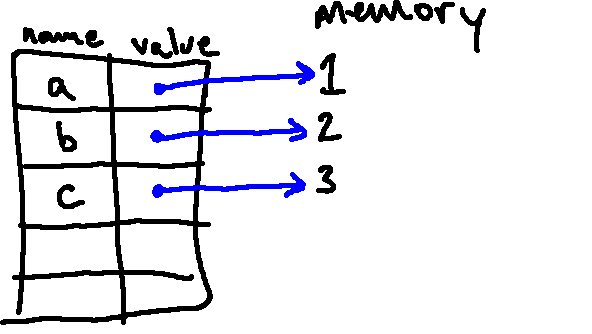
Then, when creating the first tuple, Python figures out what objects are associated with the locations in the tuple by looking up a, b, and c. As such, the entries in the tuple alias the integer objects that a, b, and c also reference:

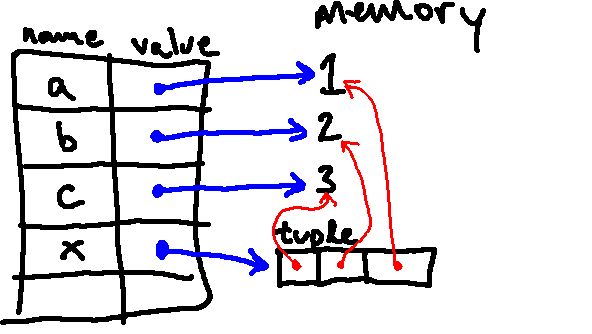
However, when creating the second tuple, Python figures out what objects are associated with the locations in the tuple by evaluating 1, 2, and 3. As such, the entries in the tuple point to different integer objects:

Try Now:

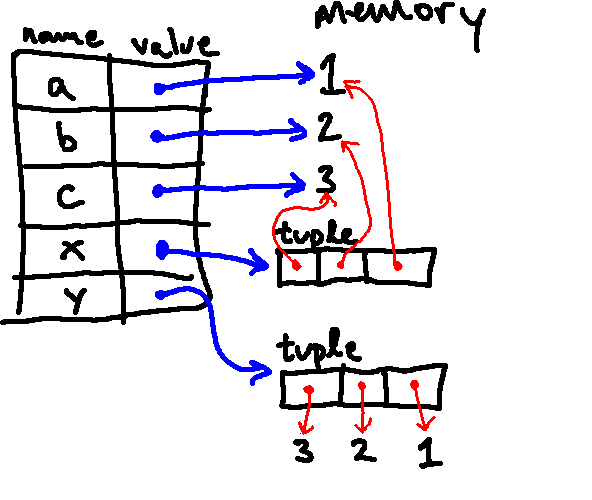
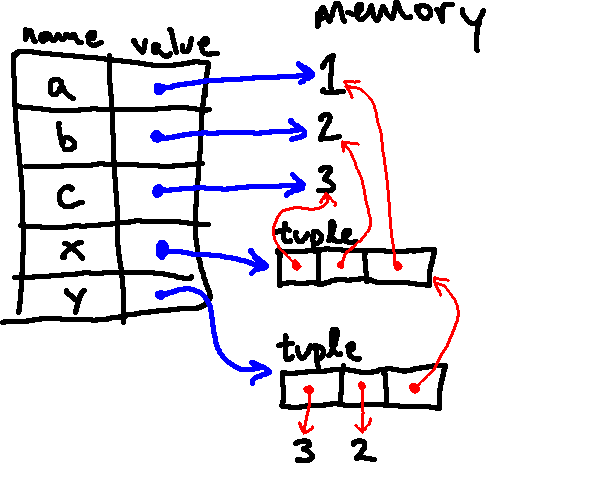
Note that tuples can contain any kind of Python object, including other tuples. So we could have had our last line instead say: y = (3, 2, x). How would the final environment diagram differ if we made this change?

Show/Hide

Here is the resulting environment diagram (notice that the only change is that y[2] and x alias the same tuple):

If we had executed this code, how would Python evaluate y[2][0]?

Show/Hide

Python would start by evaluating y and finding a tuple. It would then look up index 2 in that tuple, finding the other tuple, where it then looks up index 0, finding value 3 (the same 3 that is associated with variable c).

3.2) Lists (e.g., [7, 12, 10])

The last type of sequence we will introduce in this reading is one of the most useful built-in types, the list. Lists are almost the same as tuples, with one exception that has big potential consequences.

Like strings or tuples, lists are sequences. Like tuples, lists can contain arbitrary Python objects. This means that we can perform the same operations that we have seen previously on strings and tuples. The syntax for creating lists is similar to the syntax used for creating tuples, except that it uses square brackets instead of round brackets:

x = [None, (1, 2), "red"]

For example:

• we can use + to concatenate two lists (x + [False] which gives us a new list [None, (1, 2), "red", False]). What happens if you try to concatenate two sequences of different types (x + (1, 2, 3))?
• we can compare lists for equality ([1, 2] == [2, 1] results in False)
• we can check the length of the list (len(x) results in 3)
• we can index into a list(x[1][1] gives us the number 2)

3.2.1) Mutability

Unlike strings or tuples, however, lists are mutable; this means that they can be changed after they are created. In this section, we'll examine the effects of this difference.

With a tuple, the program below would get an error on the last line:

my_tuple = (1,2,3)
print(my_tuple[0]) # looking up elements is fine -- no error yet
my_tuple[0] = 12

Specifically, we would see the error message: TypeError: 'tuple' object does not support item assignment.

However, if we used a list instead, we could modify the elements contained in the list!

dogs = ['Lab', 'Samoyed', 'Poodle']
dogs[2] = 'Bernedoodle'
print(dogs)

['Lab', 'Samoyed', 'Bernedoodle']

We can visualize how mutating lists works using our environment diagram model. We will represent lists in environment diagrams similarly to how we represented tuples, but we will mark them clearly as lists. For example, the list [7, 12, 10] could be represented in an environment diagram as follows:

Try Now:

Draw an environment diagram for the following code, and predict what will be displayed to the screen when the following program is run. Run your code to verify; the results may be surprising!

a = [7, 12, 10]
b = [4, 5, 6]

c = a

print(a)
a[0] = 8
print(a)
print(b)
b[-1] = "cow"
print(b)
print(a)
c[1] = 3.14

print(a)

Show/Hide

After the first two lines are executed, our environment diagram should look like this:

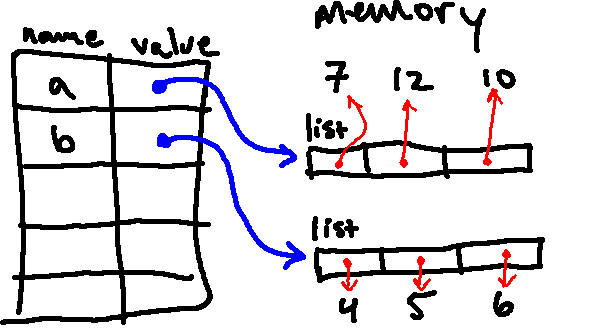
Then, importantly, when we run the next line (c = a), the names c and a are aliases for the exact same list object in memory (this does not make a copy of the list), as indicated below:

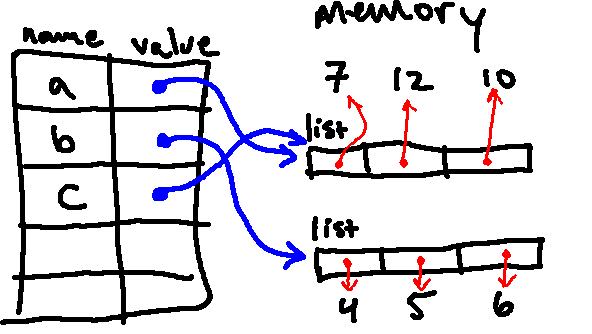
Then we print a, which will print the current value of a, which is [7, 12, 10]. The next line changes the value to which a[0] points, so we are left with:

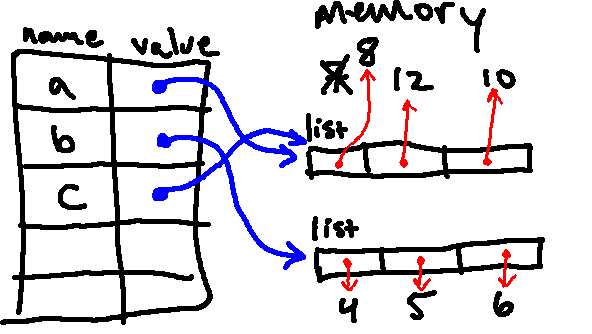
Then we print a again, which will print the updated value of a, which is [8, 12, 10]. Then we print b, which will print the current value of b, which is [4, 5, 6]. The next line changes the value to which b[-1] points, so we are left with:

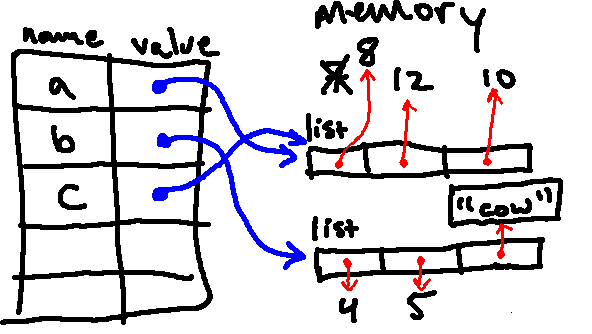
Then we print b again, which will print the updated value of b, which is [4, 5, "cow"]. Then we print a, which will print the current value of a, which is [8, 12, 10]. The next line changes the value to which c[1] points, so we are left with the following:

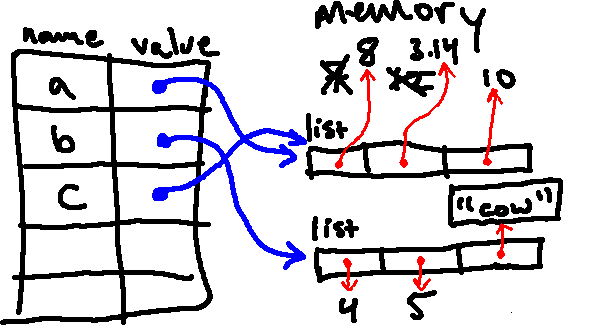
Importantly, because a and c are aliases, looking up a will also see the updated value! So when we print a, we see [8, 3.14, 10] In the end, the whole program printed the following:

[7, 12, 10]
[8, 12, 10]
[4, 5, 6]
[4, 5, "cow"]
[8, 12, 10]
[8, 3.14, 10]

3.2.2) Adding Items to a List (e.g., x.append(7))

Another common way to mutate a list is not by changing one of the elements in a list, but adding a new element to the end of the list. This is accomplished via append. For example:⁶

x = [5, 8, 3, 2, 1]
print(x)
x.append(7)
print(x)

This will print:

[5, 8, 3, 2, 1]
[5, 8, 3, 2, 1, 7]

Note that, concatenating two lists together like [1, 2, 3] + [4] creates a new list [1, 2, 3, 4] without changing the previous lists. Using the append method actually modifies the list in memory with which x is already associated. Although we sometimes have to be careful with it (because of the kinds of issues we saw above), modifying an existing list in memory is almost always substantially faster than making a new list via concatenation.

Because lists can contain arbitrary Python objects, we could use append to add any object to a list.

x.append("a string!")
x.append((7, 8, 9)) # a tuple

Try Now:

What will be printed after the following piece of code is executed?

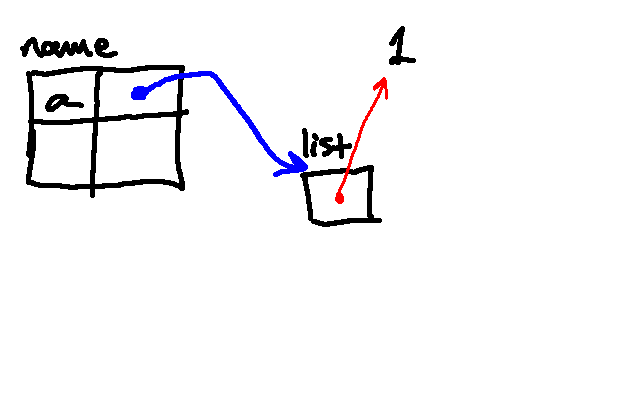
a = [1]
b = a
a.append(6)
a.append(2.0)
a.append("cat")
a[1] = "wolf"
a.append([2])
a = [4]
print(a)
print(b)

Show/Hide

The end result is that the following two values are printed:

[4]
[1, 'wolf', 2.0, 'cat', [2]]

In order to see why this is the case, let's simulate using an environment diagram. The first line creates a list containing a single element, a 1, and associates the name a with it:

The next line associates the name b with the same list in memory.

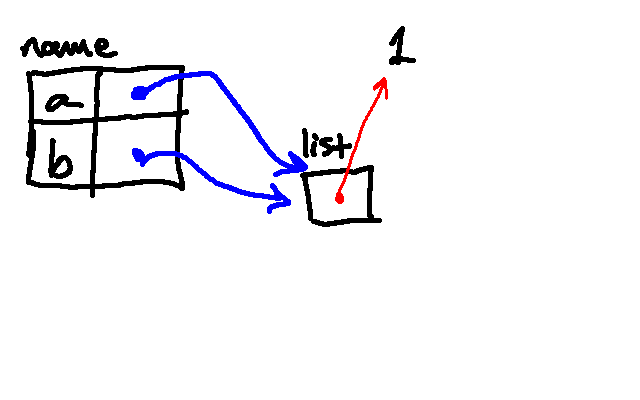
Python then looks up a and modifies the list by appending a 6 to it. Note that, because a and b are two different names for the same object in memory, the value associated with b is also changing!

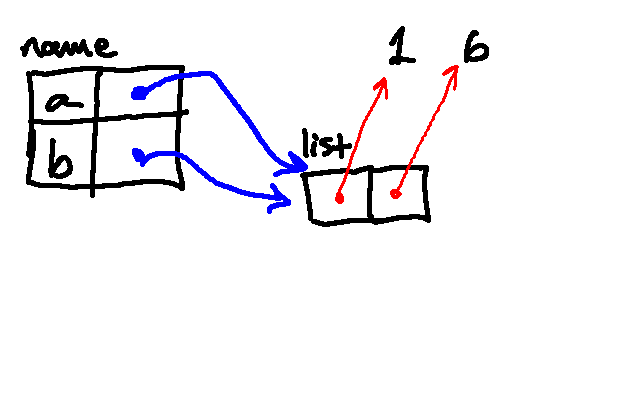
Then we append 2.0 to the same list:

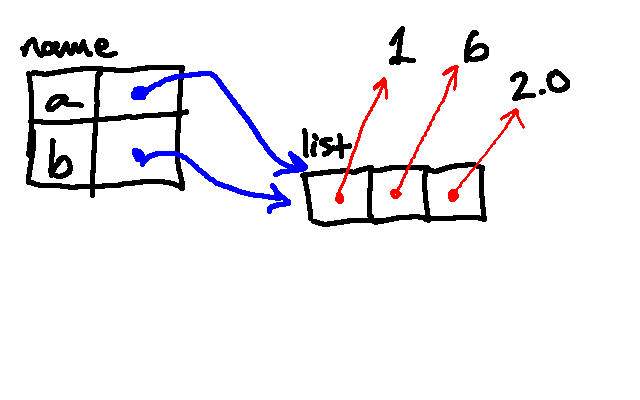
Then we append the string "cat":

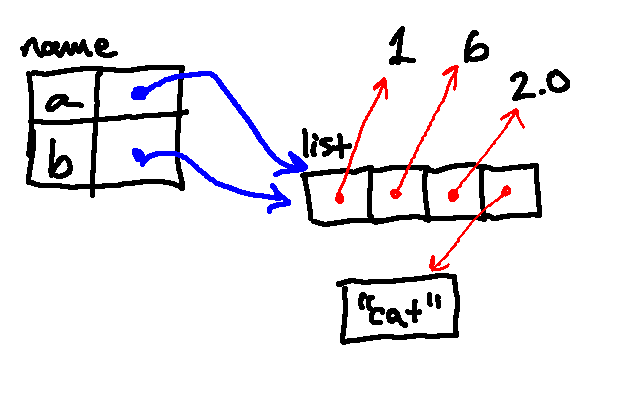
The next line then replaces the element at index 1 in the list with "wolf":

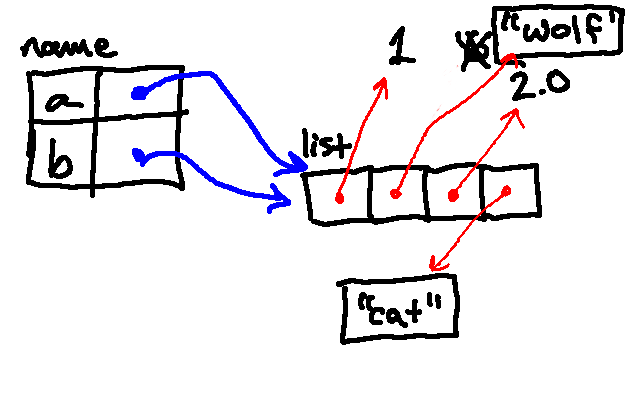
The next line then appends a list containing the number 2 to the list associated with the name a. (Notice here is an example of a list contained within another list.)

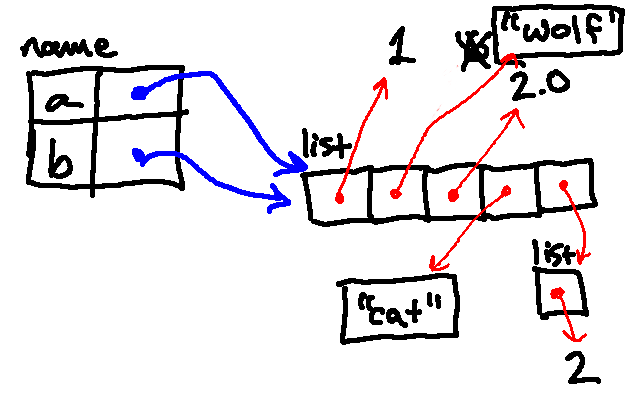
Next, we reassign a to be associated with a list containing a single 4. Note that this did not change the binding of b, which is still associated with the original list.

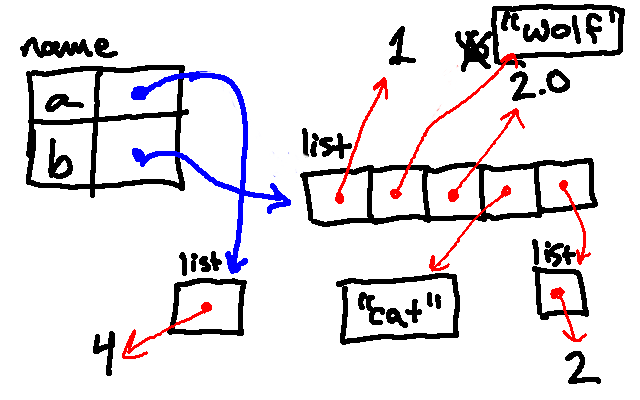
So then when we print a, Python follows its pointer and finds not the original list, but the new single-element list, and so it prints [4]. When we print b, Python follows its pointer and finds our long, modified list (despite the fact that we never explicitly told Python to do anything with b).

4) Iteration

A lot of interesting computations on sequences involve processing them one element (item) at a time. Often, they start at the beginning, select each element in turn, do something to it, and continue to the end of the sequence. This pattern of processing a sequence can be referred to as looping over the sequence.

For example, if I wanted to display each letter in a string one at a time, I could write something like the following:

word = 'cat'
print(word[0])
print(word[1])
print(word[2])
print("done!")

which would output:

c
a
t
done!

While this isn't too difficult for a short word, imagine trying to do this for a sentence, or a paragraph. This would likely involve copy, pasting, and modifying the same line of code over and over again, which in addition to being bug-prone is also difficult to read as well as modify.

Luckily, Python comes with some built in tools for iteration, which is the ability to run a block of statements repeatedly. In this section, we'll explore two such looping constructs: while loops and for loops.

4.1) While Loops

A while loop is a lot like a conditional, in that it consists of both a condition and a body and uses the condition to decide whether to execute the body, or to skip it. The difference is: whereas a conditional executed the body exactly once and moved on, a while loop will continue executing the body until the condition no longer evaluates to True. This pattern of flow is represented in this flow chart:

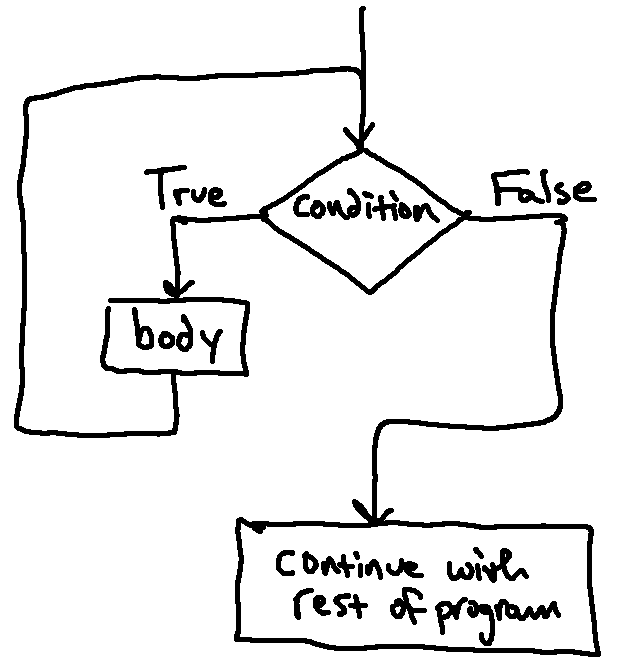
We first enter this diagram from the top. If the condition evaluates to False, then we skip the loop entirely and move on, but if it is True, we enter the body of the loop. The difference from a regular conditional is that if we do execute the body, then once we are done, we jump back and check the condition again (instead of moving on). If the condition is again True, we'll enter the loop again, and so on.

Consider the following example:

n = 5
while n > 0:
    print(n)
    n = n - 1
print('Blastoff!')

Here the condition is n > 0 and the body of the while loop contains two lines that first display the value of n and then decrement it (decrease it by one). You can almost read the while statement as if it were English. It means "While n is greater than 0, display the value of n and then decrement n. When you get to 0, display the word Blastoff!"

Slightly more formally, here is the flow of execution for a while statement:

1. Determine whether the condition is true or false.
2. If false, exit the while statement and continue execution at the next statement.
3. If the condition is true, run the body and then go back to step 1.

As written, the program above will print:

5
4
3
2
1
Blastoff!

What about our original problem of displaying every letter in a string? We could write it with a while loop as follows:

word = "cat"
i = 0
while i <= 2:
    print(word[i])
    i = i + 1
print("done!")

# now changing word will change the number of times the while loop executes!
word = "hi"
i = 0
while i < len(word):
    print(word[i])
    i = i + 1
print("done!")

4.1.1) Infinite Loops

It is important, when writing while loops, to make sure that the body of the loop changes the value of one or more variables so that the condition becomes False eventually and the loop terminates. Otherwise, the loop will repeat forever, which is called an infinite loop.⁷

In the case of the countdown program, we can prove that the loop terminates: if n is zero or negative, the loop never runs. Otherwise, n gets smaller each time through the loop, so eventually we have to get to 0.

For some other loops, it is not so easy to tell. For example:

n = 27
while n != 1:
    print(n)
    if n % 2 == 0:  # n is even
        n = n / 2
    else:  # n is odd
        n = n*3 + 1

The condition for this loop is n != 1, so the loop will continue until n is 1, which makes the condition False.

Each time through the loop, the program outputs the value of n and then checks whether it is even or odd. If it is even, n is divided by 2. If it is odd, the value of n is replaced with n*3 + 1. For example, if n starts out as 3, the resulting values of n are 3, 10, 5, 16, 8, 4, 2, and 1.

Since n sometimes increases and sometimes decreases, there is no obvious proof that n will ever reach 1, or that the program terminates. For some particular values of n, we can prove termination. For example, if the starting value is a power of two, n will be even every time through the loop until it reaches 1. The previous example ends with such a sequence, starting with 16.

The hard question is whether we can prove that this program terminates for all positive values of n. So far, no one has been able to prove it or disprove it!⁸

6
3.0
10.0
5.0
16.0
8.0
4.0
2.0

4.2) For loops

Although while loops can be used for any looping task, programmers often like having "shortcuts" to make common program patterns more concise. ⁹ A for loop is one example of a useful programming shortcut. For example, our program that prints out each letter of a string individually can be written with a for loop as follows:

# original program using while loop: 6 lines long
word = "hi"
i = 0
while i < len(word):
    print(word[i])
    i = i + 1
print("done!")

# same program using for loop: 4 lines long
word = "hi"
for i in range(len(word)):
    print(word[i])
print("done!")

Note that we did not have to explicitly set i = 0 or do i = i + 1 inside the body of the loop. The for loop handled this for us automatically. While having Python do some of the work for us behind the scenes may be a bit confusing at first, in the long run it often will save time and effort (humans are very prone to causing errors or infinite loops by forgetting to define i or increment it, but Python never forgets!)

4.2.1) Using range

In the for loop above, we called a new function range that we haven't seen before. Calling the range function creates an object that represents a sequence of integers. For example range(4) represents the sequence of integers that starts at 0 and stops just before it reaches 4.

So the program

for i in range(25):
    print(i)

will print out the numbers 0, 1, 2, ... 24 one by one and then stop before 25. Range excludes the integer we input because we often want to loop over range(len(something)), and len(something) is an index out of bounds.

i = 0
x = [1, 3, 5]
total = 0
while i <= len(x):
    total = total + x[i]
    i = i + 1
print(total)

x = [1, 3, 5]
total = 0
for i in range(len(x)):
    total = total + x[i]
print(total)

When we want to use a for loop to loop over a sequence of numbers it is important to remember to use range. If we had forgotten to call range like in the program below, we would see a new error message TypeError: 'int' object is not iterable. An iterable object is something that Python can loop over, like a sequence of objects. Python knows how to loop over the sequence of ints that range creates, but it does not know how to loop over primitive types like int, float, bool or None.

x = [1, 3, 5]
for i in len(x):
    print(x[i]**2)

4.3) When to use for vs while?

Because anything that can be written with a for loop can be written with a while loop, it can be hard to know when to use which kind of loop. Although while loops have the advantage of being explicit, for loops have the advantage of being concise, which make them easier to read. Additionally, it is a strong convention (widely used practice) among Python programmers to use for loops wherever possible. For these reasons, most of the time you should use a for loop, especially when iterating over a clearly defined sequence.

While loops are mostly used when we do not know what particular sequence of elements we want to iterate over, or how many times we would like to run through a loop. Sometimes, we want to repeat a sequence of statements until a particular condition is satisfied. An example of this will be shown in the next section where we use a while loop to approximate square roots.

4.3.1) While Example: Approximating Square Roots

While loops are often used in programs that compute numerical results by starting with an approximate answer and iteratively improving it.

For example, one way of computing square roots is Newton's method. Suppose that you want to know the square root of a. If you start with almost any estimate, x, you can compute a better estimate with the following formula:

For example, if a is 4 and x is 3:

a = 4
x = 3
y = (x + a/x) / 2
print(y)  # prints 2.16666666667

The result is closer to the correct answer (\sqrt{4} = 2). If we repeat the process with the new estimate, it gets even closer:

x = y
y = (x + a/x) / 2
print(y)  # prints 2.00641025641

After a few more updates, the estimate is almost exact:

x = y
y = (x + a/x) / 2
print(y)  # prints 2.00001024003

x = y
y = (x + a/x) / 2
print(y)  # prints 2.00000000003

In general, we don't know ahead of time how many steps it takes to get to the right answer, but we know when we get there because the estimate stops changing:

x = y
y = (x + a/x) / 2
print(y)  # prints 2.0
x = y
y = (x + a/x) / 2
print(y)  # prints 2.0

When y == x, we can stop. Here is a loop that starts with an initial estimate, x, and improves it until it stops changing:

a = 4
x = None
y = 2.5
while x != y:
    x = y
    print(x)
    y = (x + a/x) / 2

Note: For most values of a this works fine, but in general it is dangerous to test float equality (for some of the reasons we talked about in the last section, specifically that floats can't accurately represent all numbers!). Rather than checking whether x and y are exactly equal as above, it would be safer to loop until the difference between them of the difference between them becomes small enough (by comparing against some small error margin, for example: while abs(x-y) > .000001:).

4.3.2) For Example: Creating a list of squares

original_list = [7, 4, 8, 2, 9]
new_list = []  # first make an empty list to hold the results
for i in range(len(original_list)):
    num = original_list[i]  # store the element at index i
    if num % 2 == 0:  # if the number is even...
        new_list.append(num ** 2)  # add its square to the new list
print(new_list)
print(i)
print(num)

This code will proceed as follows:

• After setting original_list and new_list, Python reaches the for loop.
• The first time through the loop, Python sets i to 0 and runs the loop body.
  • It sets num = 7, because that is the element at index 0 in original_list
  • Because 7 % 2 is not equal to 0, Python does not enter the body of the conditional; rather, it moves on.
• Now, Python reassigns i to 1 and enters the loop body.
  • It sets num = 4
  • 4 % 2 == 0 evaluates to True, so we enter the body of the conditional, where we add num ** 2 (16) to the end of new_list. If we were to print new_list now, we would see [16].
• Python continues in the same way. It reassigns i to 2 and enters the loop body.
  • It sets num = 8
  • 8 % 2 == 0 also evaluates to True, so we enter the body of the conditional again, where we add 64 to the end of new_list. If we were to print new_list now, we would see [16, 64].
• Next, Python reassigns i to 3 and enters the loop body.
  • It sets num = 2
  • 2 % 2 == 0 also evaluates to True, so we enter the body of the conditional again, where we add 4 to the end of new_list. If we were to print new_list now, we would see [16, 64, 4].
• Next, Python reassigns i to 4 enters the loop body again.
  • It sets num = 9
  • Because 9 % 2 is not equal to 0, Python does not enter the body of the conditional; rather, it moves on.
• Because the next number in the sequence is 5 which is the len(original_list), Python exits the loop and continues to the statement: print(new_list). Printing new_list displays the following to the screen:

  [16, 64, 4]
  

• Next, it executes the statement print(i), which displays 4, the current value that i was assigned to.
• Next, it executes the statement print(num), which displays 9, the current value of num.

Even though i and num were defined inside the loop, Python created those variable names in the global frame, so that when we look up those variables again after the loop, it remembers their values!

One last note about loops: using i as our loop variable is a Python convention (i is short for index). In future readings we will see other loop variations with other loop variable names.

5) Debugging

In this reading, we have introduced some new structures, and started moving toward more complicated programs, which can be more difficult to think about. In general, we can attempt to manage this complexity by trying first to break our programs down into small pieces, which can be written and tested independently of the others (this is referred to as modular design because we are thinking of splitting the program into separable modules). It is generally much easier to plan, test, and implement individual pieces as you go, rather than to spend hours writing a big program, and then find it does not work, and have to sift through all your code, trying to find the bugs.

However, even with all the clever design in the world, you will still occasionally find yourself in the (inevitable) position of having a big program with a bug in it; in that case, do not despair! Debugging a program does not usually require brilliance or creativity or much in the way of insight. What it requires is persistence and a systematic approach, because it requires reasoning not only about what we want, but about how Python will behave in response to our programs (this is why it's so important to have a strong mental model of Python!).

First of all, it is crucial to have a test case (a set of inputs to the program you are trying to debug) and to know what the answer is supposed to be, both for the overall program and for relevant intermediate values. To find a good test case, you might start with some special cases: what if the argument is 0 or the empty list? What if it is negative? Those cases might be easier to sort through first (and are also cases that can be easy to get wrong). Then try more general cases.

For most programs in this class, you should simulate your code by hand using an environment diagram before running it in Python. We know this is tedious, but it really is important for helping you build a strong mental model of how Python behaves. With more experience, you will be able to make these predictions quickly in your head. But for now, draw it out!

Then the question remains: if your program gets your test case(s) wrong, what should you do? Resist the temptation to start changing your program around, just to see if that will fix the problem. Do not change any code until you know what is wrong with what you are doing now, and therefore believe that the change you make is going to correct the problem.

We have a few tools available to us already to this end, which can work reasonably well for small programs: the substitution model for expression evaluation, and environment diagrams. The act of simulating with these tools may help you find your error. It is important to remember that Python doesn't know what you want to do, only what you tell it to do, so you must be systematic when going through your code.

Sometimes, you may not be able to find your bug on paper. For those cases, the method we'll advocate centers around debugging systematically using print statements. It is worth noting that nowadays there exist tools other than print to help with debugging (logically called debuggers), but it is very rare even after years of experience programming that we find the need to use such a tool. In our minds, print is still the most straightforward, most powerful, and most general debugging tool in existence.

One good way to use print statements to help in debugging is to use them to display the results of intermediate steps along the way. Depending on the structure of your program, this might be: the values you are looping over (to make sure your bounds are correct), a complete solution to a subproblem, a partial solution to the overall problem. For your chosen location(s), you should print both the quantity of interest and the value you expect that quantity to have. If they are the same, it may be that that part of the code is working properly, and you can try printing in other locations.¹⁰

One strategy here is to use a variation on binary search. Find a spot roughly halfway through your code at which you can predict the values of variables, or intermediate results your computation. Put a print statement there that lists expected as well as actual values of the variables. Run your test case, and check. If the predicted values match the actual ones, it is likely that the bug occurs after this point in the code; if they do not, then you have a bug prior to this point (of course, you might have a second bug after this point, but you can find that later). Now repeat the process by finding a location halfway between the beginning of the procedure and this point, placing a print statement with expected and actual values, and continuing. In this way you can narrow down the location of the bug. Study that part of the code and see if you can see what is wrong. If not, add some more print statements near the problematic part, and run it again.

The most important rule of debugging is: Don't try to be smart; be systematic and indefatigable! And don't despair!

6) Syntatic Sugar: Sequence Operations

The previous sections have covered all the content you need to know for this unit's assignments. However, in this (and future) readings, we will provide some additional instruction about other Python features that can provide additional "shortcuts" which allow you to write more concise code. Knowing about "syntatic sugar" (another term commonly used for Python shortcuts) may come in handy both because they will empower you to write more concise code and because more experienced Python programmers often use these commands and so they may appear "in the wild" (online or in other courses). However, we encourage you to master the fundamentals we describe above before diving into using lots of fancy syntax.

6.1) Sequence Comparisons (>=, <=, >, <)

It's important to note that in Python the greater/less comparisons (>=, <=, >, <) can only be made between sequences of the same type.

6.2) String Methods: upper, lower, and replace

Python has many useful methods that are unique to strings (like how append is unique to lists). A few string methods to note are:

.upper(): Returns a new copy of the string with all the cased characters converted to uppercase.¹¹

For example:

>>> 'hello123'.upper()
'HELLO123'
>>> 'this is too LOUD!'.upper()
'THIS IS TOO LOUD!'

.lower(): Returns a new copy of the string with all the cased characters converted to lowercase.

For example:

>>> 'NO CAPS?'.lower()
'no caps?'
>>> "WHAT??? WHY aren't HATS allowed?1?".lower()
"what??? why aren't hats allowed?1?"'

.replace(old, new[, count]): Return a new copy of the string with all occurrences of substring old replaced by new. If the optional argument count is given, only the first count occurrences are replaced.

For example:

>>> "jar jar".replace("j", "c")
'car car'
>>> "cheese".replace("e", "o", 2)
'choose'

There are many more useful string methods described in the python documentation!

6.3) Converting Between Types (list(x), str(x), tuple(x))

In the last set of readings, we saw that we could convert between int and float objects (for example, with int(7.8) or float(6)).

It is also possible to convert between strings and numeric types, provided we are dealing with strings in a particular form. For example:

• str(6.0) will give us the string "6.0".
• int("2") will give us the integer 2.
• float("7.8") will give us the float 7.8.

We can also convert sequences to other sequences:

>>> list("abc")
['a', 'b', 'c']
>>> str([1,2,3])
'[1, 2, 3]'
>>> tuple(range(4))
(0, 1, 2, 3)

6.4) Other Common Sequence Operations

While strings, tuples, and lists have unique properties (strings only contain characters and are immutable, tuples can contain any object but are immutable, lists can contain any object and are mutable), by design they also share many similar properties (they are all ordered collections of objects), operations, and behaviors.

In addition to the shared behaviors of concatentation, comparison, len and indexing, we can also:

• multiply a sequence by an int using *. For example, [0] * 3 will create a new list [0, 0, 0].
• check if a sequence contains some value using in or not in. For example

>>> "h" in "horse"
True
>>> "!" not in ["a", 1, 2]
True
>>> (4, 3, 2) in (4, 3, 2)
False

Note that the in operator works differently depending on the object type. element in some_list evaluates to True if any equivalent object to element (compared via ==) exists as one of the elements in the list represented by some_list. element in some_tuple behaves the same way. some_string in some_other_string behaves differently: it will evaluate to True if the string some_string is a substring of the string some_other_string.

• slice into sequences to create new sequences. For example:

x = ["a", "b", "c", "d", "e"]
print(x[0:2])   # ["a", "b"], equivalent to x[:2]
print(x[2:5])   # ["c", "d", "e"], equivalent to x[2:] or x[-3:]
print(x[:])     # ["a", "b", "c", "d", "e"], x[0:5] creates a copy
print(x[100:])  # [] note that slicing out of bounds does not raise an error!
print(x[0:5:2]) # ["a", "c", "e"], equivalent to x[::2]
print(x[::-1])  # ["e", "d", "c", "b", "a"], reverse copy

Note slicing in general has a pattern of [start_index : stop_index : step] By default, the start_index is 0, the stop_index is the length of the sequence, and the step size is one (which is why you can omit some of the numbers and still get the same result). A step size of 2 in the second to last example means that the element at every other index between 0 <= i < 5 will be included (so 0, 2, 4). Try to experiment with slicing into strings and tuples!

There are other common sequence operations, which you can learn more about by reviewing the official Python documentation here.

7) Summary

In this reading, we introduced a few kinds of compound objects (strings, tuples, and lists) and began to expand upon the ideas introduced earlier, by introducing new ways of controlling the order in which Python executes statements (for and while), and using these to give more powerful ways to manipulate compound objects.

In this week's exercises, you'll get some practice with these new pieces, as well as some review on the older pieces.

In the next set of readings and exercises, we will introduce more tools and a powerful Python built-in type: the dictionary.